Organization:
1. Standardisierung einer Zufallsvariablen
2. Lineare Regression
3. W-keitserzeugende Funktion
4. Charakteristische Funktion
5. Der zentrale Grenzwertsatz
Standardisierung einer Zufallsvariablen
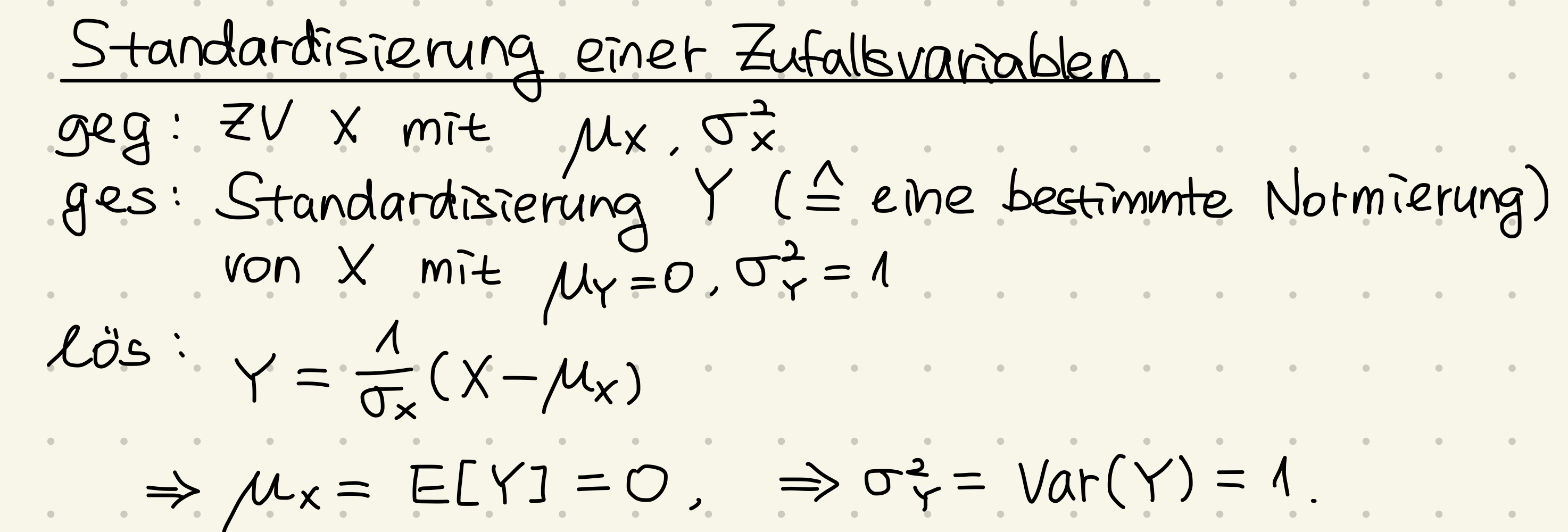
Lineare Regression

10.1 Wahrscheinlichekeitserzeugende Funktion
für \( X : \Omega \rightarrow \mathbb{N}_0\), diskrete Zufallsvariablen
$$ G_X(z) = E[z^X] = \sum^{\infty}_{k = 0}\ p_X(k)z^k , \qquad |z| \leq 1 $$
Anwendungen:
- Wahrscheinlichkeitsverteilung:
$$ p_X(n) = \mathbf{P}(\{ X = n \}) = \cfrac{1}{n!} \begin{bmatrix} \cfrac{d^n}{dz^n} G_X(z) \end{bmatrix}_{z = 0} \quad \forall n \in \mathbb{N}_0 $$
- Erwartungswert:
$$ E[X] = \begin{bmatrix} \cfrac{d}{dz} G_X(z) \end{bmatrix}_{z = 1} $$
$$ E[X^2] - E[X] = \begin{bmatrix} \cfrac{d^2}{dz^2} G_X(z) \end{bmatrix}_{z = 1} $$
- Varianz:
$$ Var[X] = \begin{bmatrix} \cfrac{d^2}{dz^2} G_X(z) \end{bmatrix}_{z = 1} - E[X]^2 + E[X] $$
- Für \( X_i : \Omega \rightarrow \mathbb{N}_0, \ i \in \{1, 2, ... , n \} \) stochastisch unabhängige, diskrete, nichtnegative ZV und Z \( \sum^n_{i = 1} X_i \)
$$ G_Z(z) = \prod^n_{i = 1} G_{X_i}(z) $$
10.2 Charakteristische Funktion (stetige ZV!!)
$$ \varphi_X(\omega) = E[e^{i \omega X}], \quad \omega \in \mathbb{R} $$
$$ \varphi_X = \int^{\infty}_{- \infty} e^{i \omega x} \ f_X(x) dx $$
\( f_X(-x) \circ-\bullet \varphi(\omega) \)
\( f_X(-x)\) entspricht gespiegelter Fouriertransformation !
- Erwartungswert / \(n\)-tes Moment:
$$ E[X^n] = \cfrac{1}{i^n} \begin{bmatrix} \cfrac{d^n}{dz^n} \varphi_X(\omega) \end{bmatrix}_{\omega = 0} $$
- Summe von ZV :
$$ \mbox{für} Z = \sum^n_{i = 1} X_i, \ X_i \mbox{stochastisch unabhängig} $$
$$ \varphi_Z(\omega) = \prod^n_{i = 1} \varphi_{X_i}(\omega) $$
10.3 Der zentrale Grenzwertsatz
Definition: Seien \(X_i, \ i \in 1, ... , n \), stochastische unabhängie & identische verteilte reelle Zufallsvariablen und gelter \(E[X_i] = \mu < \infty \) und \( Var[X_i] = \sigma^2 < \infty \). Dann konvergiert die Verteilung der standardisierten Summe
$$ \mathbf{Z}_n = \sum^n_{i = 1} \cfrac{(X - \mu)}{\sigma \sqrt{n}} $$
das heißt: \( E[\mathbf{Z}_i] =0 \) und \( Var[\mathbf{Z}_n] = 1\). für \(n \rightarrow \infty \) gegen die Standardnormalvertilung.
Es gilt also:
$$ \lim_{n \rightarrow \infty} \mathbf{P}(\mathbf{Z}_n \leq z) = \Phi(z) $$



댓글