Organization
1. Markow-Ungleichung
2. Tschebyschow-Ungleichung
3. Das schwache Gesetz der großen Zahlen
4. Bedingte Unabhängigkeit
5. Markowketten
11.4 Markow-Ungleichung
마르코프 부등식은 확률론에서 평균 정보를 이용해(= 기댓값) 자료가 어떤 구간에 위치할 확률이 얼마나 되는 지를 표현할 수 있는 공식이다.
어떠한 자료 X에 대한 E[X]와 Var[X]가 주어졌다고 가정하자. 이때 자료 X가 특정 구간에 위치할 확률이 임의의 식으로 나타낼수 있는가? 아니다, 왜냐하면 확률분포에 따라 답이 그때그때 달라지기 때문이다. 예를들어 X가 Normalverteilung/정규분포를 따른다고 하면, X가 임의의 수 x보다 작을 확률은 평균이 0 이고 분산이 1인 표준정규분포를 따른다. 그리고 이에 의해 표준화변수 Z로 바꿔주는 표준화 공식에 의해 변환이 가능하며 따라서 X가 특정 구간에 위치할 확률을 얻을 수 있다.
$$ \mathbf{P}(\{ |X| \geq a \}) \leq \cfrac{E[|X|]}{a} $$
Es gilt: \(E[|X|] < \infty, a > 0 \)
중요한 조건은 자료 X가 항상 음이 아니어야 한다는 것이다. 마르코프 부등식은 다시 말해 확률분포가 없어도 어떤 확률을 근사하게 추정 가능하다는 것이다. 애초에 마르코프 "부등식"이므로 정확한 관계식이라기 보다는 얼추의 범위를 표현 할 수 있다는 것이 한계점이다.
그러나 바로 다음에 소개되는 Tschebyschow-Ungleichung/ 체비쇼프 부등식은 마르코프 부등식과 분산, 평균을 이용해 보다 더 정확한 값의 추정치를 구할 수 있다.
11.5 Tschebyschow-Ungleichung
$$ \mathbf{P}(\{|X - E[X]| \geq a \}) \leq \cfrac{Var[X]}{a^2} $$
Es gilt: \( Var[X] < \infty , \ a > 0\)
그러나 단점이 하나 있는데, 자료 X의 확률분포가 평균을 기준으로 대칭이라고 가정을 해야 한다는 점이다. 그러나 모든 분포가 대칭이지는 않다. 이에 반하는 예시를 위해 Borel-Cantelli Lemma 혹은 One-sided Tschebyschow Ungleichung이 있다.
Markow- & Tschebyschow- Ungleichung geben jewils eine obere Schranke für die Wahrscheinlichekeit an, dass eine nichtnegative Zufallsvariable einem Wert größer als eine positive Konstante \(a\) annimmt.
11.6 Das schwache Gesetz der großen Zahlen : Law of Large Numbers (L.L.N)
sei \( X_i : i \in \mathbb{N}\) eine Folge reeller, paarweise unkorrelierter Zufallsvariablen mit beschränkter Varianz. Dann gilt:
$$ \cfrac{1}{n} \sum^n_{i = 1} (X_i - E[X_i]) \rightarrow 0 $$
Für stochastisch unabhängige und identisch verteilte Folgenelemente mit \( E[X_i] = E[X] \mbox{ und } Var[X_i] = Var[X] < \infty \) gilt:
$$ \cfrac{1}{n} \sum^n_{i = 1} (X_i) \rightarrow E[X_i] $$
\( \rightarrow \) Antwort auf die Frage, ob und wogegen der arithmetischen Mittelwert eienr Zufallsfolge konvergiert.
\( \rightarrow \) "Schwaches Gesetz", weil von Konvergenz in W-keit.
예를 들어 동전을 \(n\)번 던지는 것을 상상해보자,
unabhängige und identisch verteilte (영어로 i.i.d.)한 Zufallsvariablen \(X_i, \forall i \in \mathbb{N}\)가 존재하고 확률 변수들의 분포가 베르누이의 법칙을 따른다고 가정하면, \(X_i\)를 동전 앞면이 나올때를 1, 뒷면이 나왔을 때를 0 으로 볼 수 있다. 이때 표본의 평균 \( \bar{X_i} \)이라 하고 이것은 동전을 \(n\)번 던졌을때 동전 앞면이 나오는 횟수 라고 볼 수 잇다.
\( \rightarrow\) SLLN(Strong Law of Large Numbers)의 관점에서 생각하면 동전을 많이 던질수록 ( \(n\) 의 증가) 표본평균 \( \bar{X_i} \)가 Population Mean(= \(\mu = \cfrac{1}{2}\) ) 에 수렴할 확률은 1이다.
\( \rightarrow \) WLLN(Weak Law of Large Numbers)의 관점에서 생각하면 동전을 많이 던질수록 ( \(n\) 의 증가) 표본평균 \(\bar{X_i} \)과 popultation mean(= \(\mu = \cfrac{1}{2}\) )의 차이가 임의의 양수 \( \epsilon \) 보다 클 확률이 점점 작아져 0에 수렴한다.
14. Bedingte Unabhängigkeit
14.1 Bedingte Unabhängigkeit

\( \rightarrow \) Das Eintreten von Ereignis C liefert keine Mehrinformation über Wahrscheinlichkeit von A, wenn wir wissen, dass B eintritt.
12. Markowketten : Markow Chains
12.1. Markowketten
12.1.1. Allgemein
Eine Zufallsfolge( \( (X_n : n \in \mathbb{N}) \) ) heißt, Markowkette, falls \( \forall n_i \in \mathbb{N} , \ i \in 1, 2, ..., k, \mbox{ mit } n_1 < ... < n_k \) gilt:
$$ (X_{n_1}, X_{n_2}, ... , X_{n_{k-2}}) \rightarrow X_{n_{k-1}} \rightarrow X_{n_k} $$
\(\Rightarrow \) Die Verteilung eines Folgeelements hängt nur vom direkten Vorgänger ab
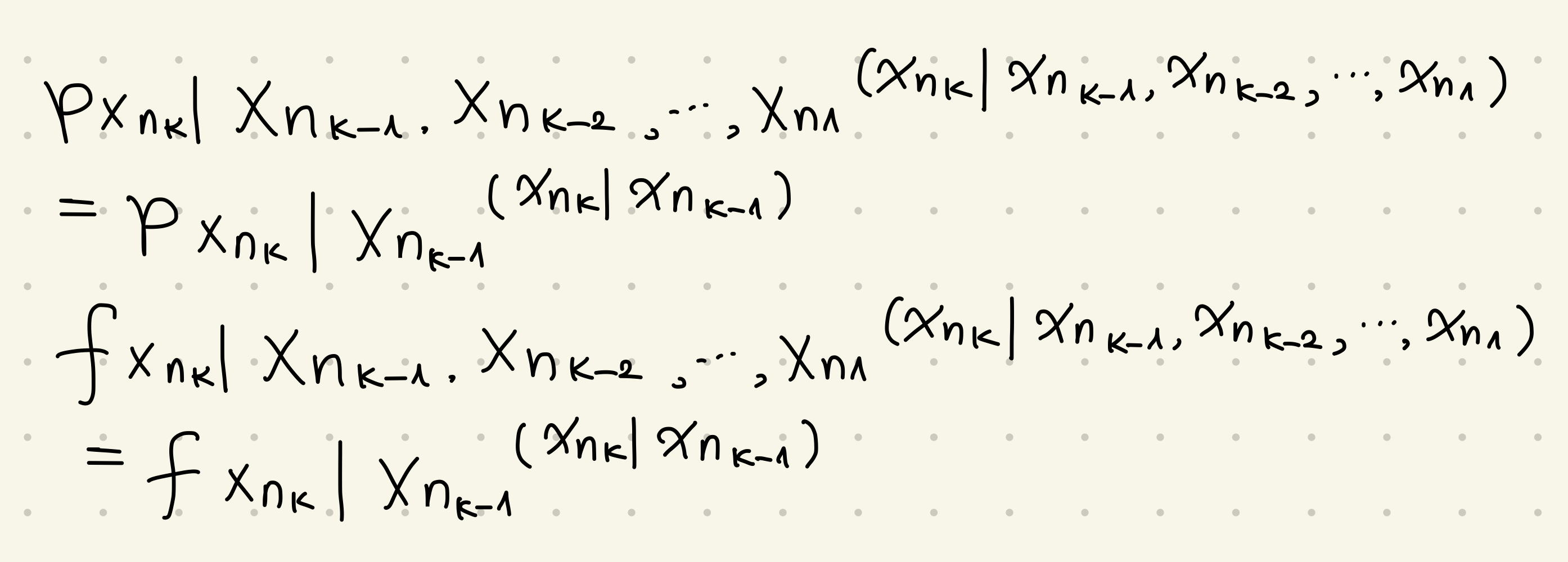
\( \rightarrow \) Markow-Eigenschaft in Warten: bedingt auf ein gegebenes \(X_{n -1}\) ist das nachfolgende Element \( X_n \) bedingt unabhängig von \( X_1, X_2, ... , X_{n-2}\)
\( \rightarrow \) Interpretation, wenn man sich Zufallsfolge als zeitliche Abfolge von Zufallsvariblen versteht:
Zusätzlich Kenntnis der gesamten Vorgeschichte \( X_1, ..., X_{n-2}\) der Zufallsfolge bringt keine zusätzliche Kenntnis über \(X_n\)


댓글