Uninformed Search
Organization
1. Formulating Problems
2. Example Problems
3. Searching for Solutions
<next post>4. Uninformed Sercha Strategies1) Breadth-First Search2) Uniform-Cost Search (Dijkstra's algorithm)3) Depth-First Search4) Depth-limited Search5) Interative Deepening Search6) Bidirectional Serach5. Comparision and Summary
Motivation

One example how search is used in research gruop:
- Automated vehicles have to search a collision-free path from a start to a goal configuration.
- Searching in continuous space is difficult.
- We discretize the search problem in space and time by offering only a finite number of possible actions at discrete time steps.
This makes it possible to use classical sesarch techniques.
Example: Holiday in Romania
1. Currently in Arad
2. Flight leaves tommorrow from Bucharest.

A problem can be formally defined by 5 components;
| Components | Example: Holiday in Romania |
| The initial state the agent starts in | Arad |
| The possible actions | IN(Arad) are GO(Sibiu) , GO(Timisoara) , GO(Zerind) |
| What each action does, which we refer to as the transition model |
RESULT(IN(Arad) , GO(Zerind)) = IN(Zerind) |
| The goal test, which checks whether a given stateis the goal state. | IN(Bucharest) |
| A path cost function assigning a numeric cost to each solution path. | traveled distance is a good path cost. |
Vacuum-Cleaner World
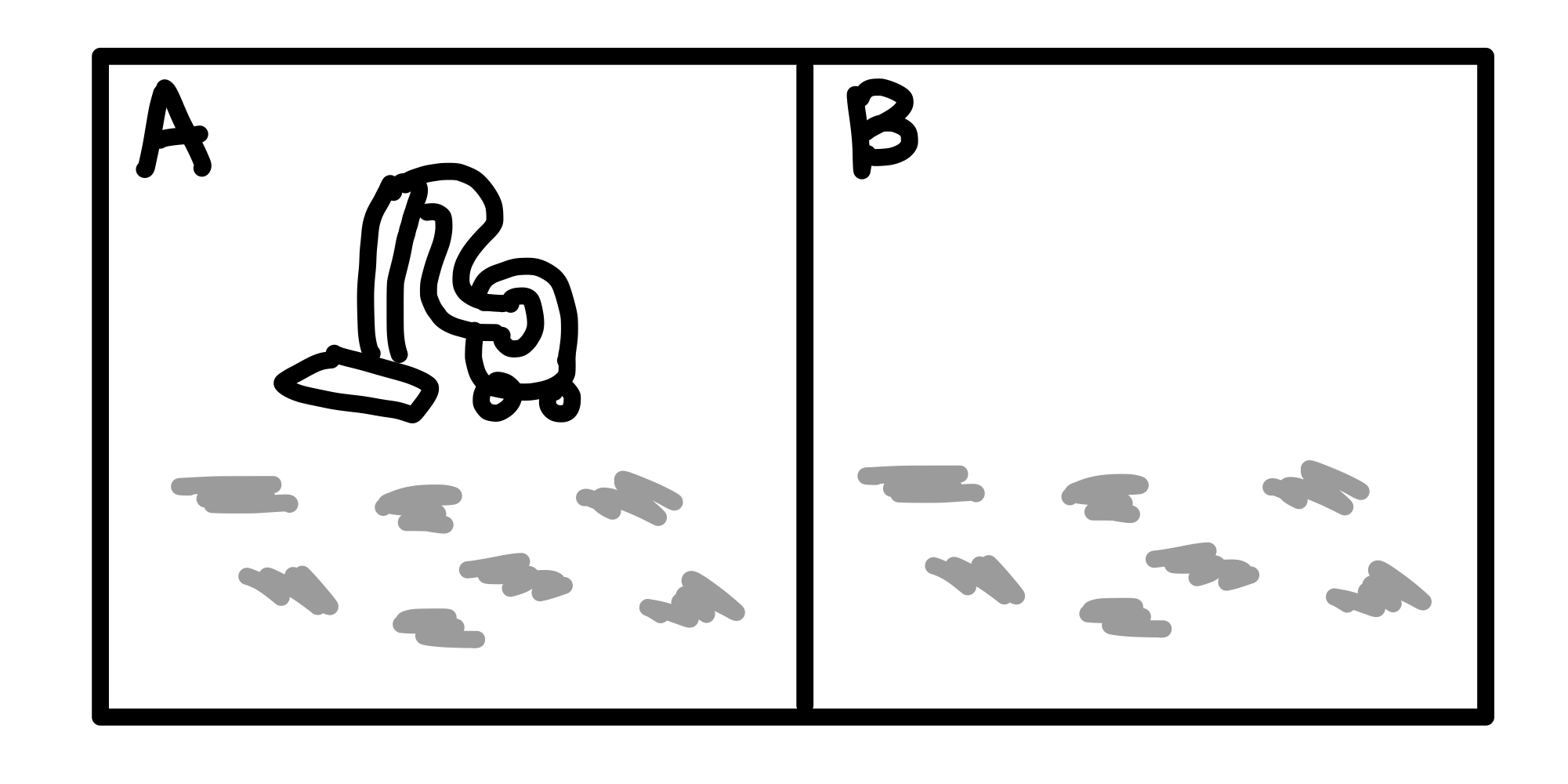
| Percepts | location and contents, e.g., [A, Dirty] |
| Actions | Left, Right, Suck, NoOperation |
Holiday in Romania
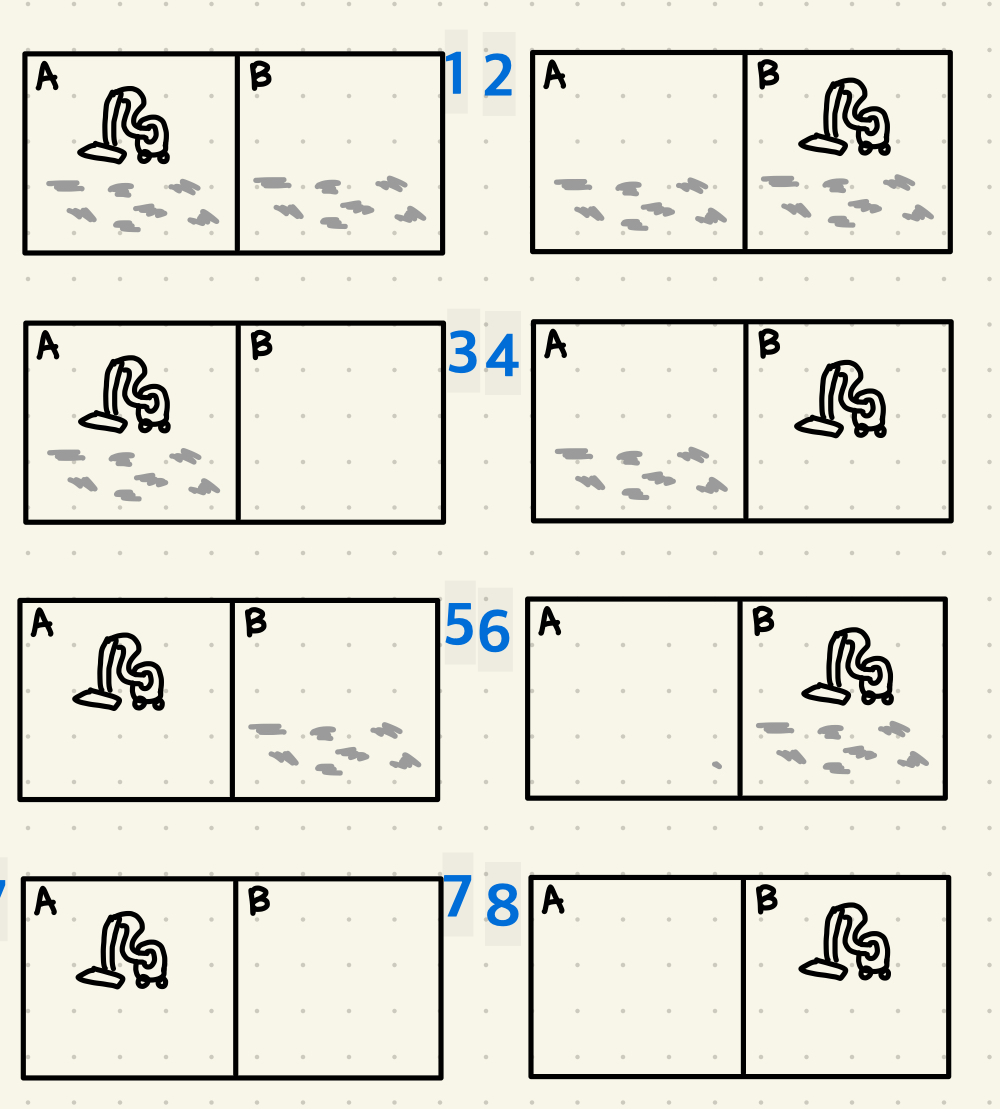
- States: Combination of cleanr and dirt locations: $$ 2 \bullet 2^{2} $$
- Initial State : any state
- Actions: Left, Right, Suck
- Transition model:
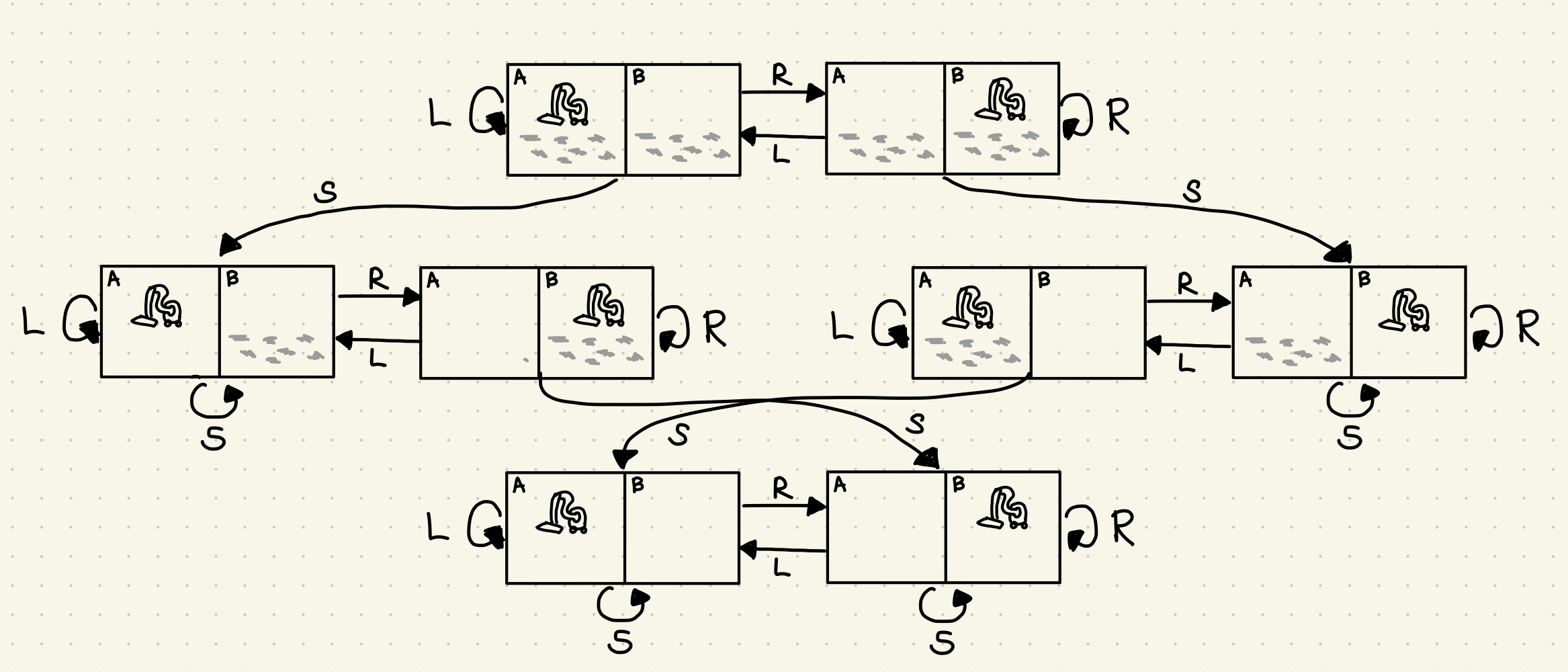
Transition model can be stored as as directed graph, just like the Holiday-in-Romania-Problem.
This is possible for all discrete problems.
- Goal test: check whether all locations are clean.
- Path cost: Each step costs 1.
8-Puzzle

Tiles can move to the blank space. How to reach the goal state?
- States: Specify the location of each tile and the blank space:
$$ \frac{9!}{2} $$ = 181440 states. / 초기 상태의 반만 goal 상태로 이동 가능하다.
- Initial state: Any state
- Actions: Movement of the blank space: Left, right, Up, down
- Transmition model: Huge, but trivial e.g., if Left applied to start state: '5' and 'blank' are swichted
- Goal test: Checks whether toe goal configuarion is reached.
- Path cost: Each step costs 1.
8-Queens Problem

- Place 8 queens on a chessboard such that no queens attack each other. A queen attacks any piece in the same row, column or diagonal
- Is the above figure a feasible solution?
여기서 Solution이란 Answer와는 차이가 있다. Answer는 답을 지칭하지만 Solution은 답이 유도된 풀이까지를 모두 지칭한다. 이 전체의 풀이 과정을 우리는 Algorithm_알고리즘 이라 부른다. 이후에 설명을 따라가면 결국 알고리즘이란, Initial State(초기상태)에서 Goal State(목적지)까지의 여정을 말한다.
- Two formulations:
1) Incremental formulation: Start with an empty chessboard and add a queen at a time.
2) Compete-state formulation: Start with 8 queens and move them.
We try the following INCREMENTAL FORMULATION:
- State: Any arrangement of 0 - 8 queens:
- Initial state: No queens on the board.
- Actions: Add a queen to any empty square.
- Transition model: Returns the board with a queen added to the specified square.
- Goal test: 8 queens on the board, none attecked.
- Path cost: Does not apply.
Improvement to reduce complexity: Do not place a queen on a square that is already attackted.
- State*: Any arrnagement of 0 - 8 queens with no queens attacking each other in the n leftmost colunms.
- Actions* : Add a queen to any empty sqaure in the leftmost empty colunm such that it is not attacked by any other queen.
이런 여러가지 예시를 통해 우리는 어떤 문제를 마주치는지 알아보았다. 그럼 이렇게 마주한 문제들을 어떻게 풀어가는 것이 좋을까?
가장 기본적인 접근 방법은 익히 알고 있는 Search Tree 이다.
Generating a Search Tree
Search Tree is an action sequence to a goal state.
- Root : Initial state
- Branches : Actions
- Nodes : Reached states.
- Leaves: Unexpanded nodes.

A search tree is expanded by applying all possible actions to each parent node.
Tree Search Algorithm
funktion Tree-Search (problem) returns a solution or failure
initialize the freontier using the initial state of problem
loop do
if the frontier is empty then return failure
choose a leaf node and remove it from the frontier
if the node contains a goal state then return the corresponding solution expand the chosen node, adding the
resulting nodes to the frontier.
Avoiding Loops in the Search Tree is important.
In the previous Search Tree for Holiday in Romania, we went back to Arad from Sibiu: Expanding from Arad only contains repetitions of previous possibilities.
Solution: Only expand nodes that have not been visited before. Visited states are stored in an explored set or closed list.
Graph Search Algorithm
funktion Graph-Search (problem) returns a solution or failure
initialize the freontier using the initial state of problem
initialize the explored set to be emtpy
loop do
if the frontier is empty then return failure
choose a leaf node and remove it from the frontier
if the node contains a goal state then return the corresponding solution
add the node to the explored set
expand the chosen node, adding the resulting nodes to the frontier only if not in frontier or explored set
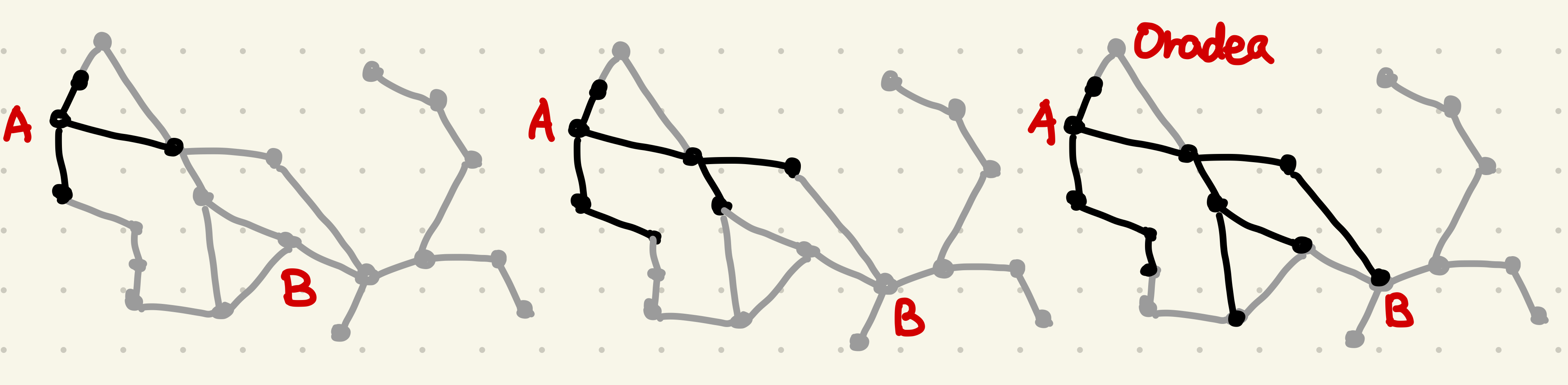
마지막 일러스트처럼 가장 윗쪽의 점이 Oradea는 dead end가 된다. 그 이후의 액션이 존재하지 않기 때문이다.
Search Tree처럼 방법을 평가할때 이 문제 해결 방법이 괜찮은가를 평가하는 기준 4가지가 존재한다.
Measuring Problem-Solving Performance
We can evaluate the performance of a sesarch algorithm using the following criteria:
- Completeness: Is is guaranteed thath the algorithm find a solution if one exists?
- Optimality: Does the strategy find the optimal solution? = minimum cost !
- Time complexity: How long does it take to find a solution?
- Space complexity: Howh much memory is needed to perform the seaerch?
Infrastructure for Search Algorithm
Structure of a node n
n.STATE : node가 있는 곳의 상태
n.PARENT : 어떤 노드를 생성한 노드 (부모)
n.ACTION : 노드를 생성할때 한 행동
n.PATH-COST : $$ g(n) $$, 초기 상태부터 시작한 모든 길
Operations on a queue(_줄,대기) = list of elements
Empty(queue) : Returns true if queue is empty
Pop(queue) : Removes the first element of the queue and returns it;
Insert(element, queueu) : Inserts an element and returns the resulting queue.
Obtaining the Solution
- Obtain solution(i.e. state and action sequence) by iterating backwards over parents. / 뒤로 반복해서 솔루션을 얻는다.
- Apply actions forward to reach the goal / 앞으로 반복해서 솔루션을 얻는다.

State sequence: A, ..., C, G
Action sequence: \( {\gamma}, .... , {\mu} \)
'All About ECE > Artificial Intelligence' 카테고리의 다른 글
| [AI/인공지능] Informed Search (0) | 2022.12.16 |
|---|---|
| [AI/인공지능] Depth-Limited Search, Interactive Deepening Search, Bidirectional Search, Uninformed Search Summary (0) | 2022.12.16 |
| [AI/인공지능] Breadth-First Search, Uniform-Cost Search, Depth-First Sesarch (0) | 2022.12.16 |
| [AI/인공지능] Intelligent Agents (0) | 2022.12.14 |
| [AI/인공지능] Introduction to AI (0) | 2022.12.14 |



댓글