Uninformed Search - 3/3
Organization
<previous post>1. Formulating Problems2. Example Problems3. Searching for Solutions4. Uninformed Sercha Strategies1) Breadth-First Search2) Uniform-Cost Search (Dijkstra's algorithm)3) Depth-First Search
4) Depth-limited Search
5) Interative Deepening Search
6) Bidirectional Serach
5. Comparision and Summary
Depth-limited Search
Shortcoming in depth-first search: Depth-first search does not terminate in infinite state spaces. / DFS는 무한한 노드가 있을 경우 프로세스가 끝나지 않는다.
Solution: to make a depth limit.
function Depth-Limited-Search returns a solution or failure/cutoff
return Recursive-DLS(Make-Node(problem.Initial-State), problem, limit)
/ DLS는 DFS를 보완해서 만든 탐색으로, 깊이의 제한이 추가된다.
- 자식들에 대해 탐색한 결과값이 cutoff 라면, 길이 제한으로 인해 더 이상 탐색 X
- 자식들에 대해 탐색한 결과값이 failure 라면, 계속 탐색을 진행한다.
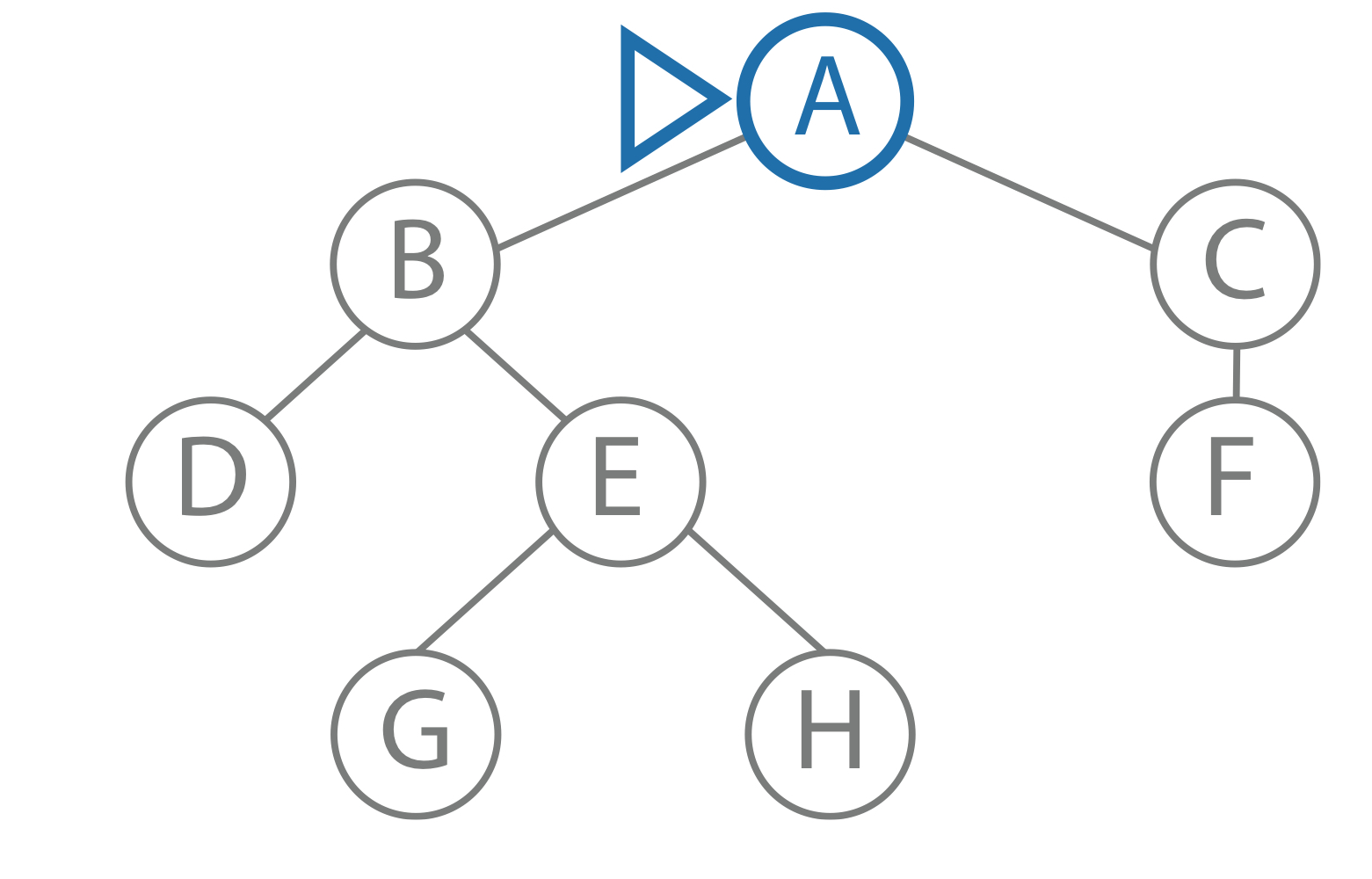 |
goal: F limit: 2 current path: A node: A child: B result: to be computed |
 |
goal: F limit: 1 current path: A ,B node: B child: D result: to be computed |
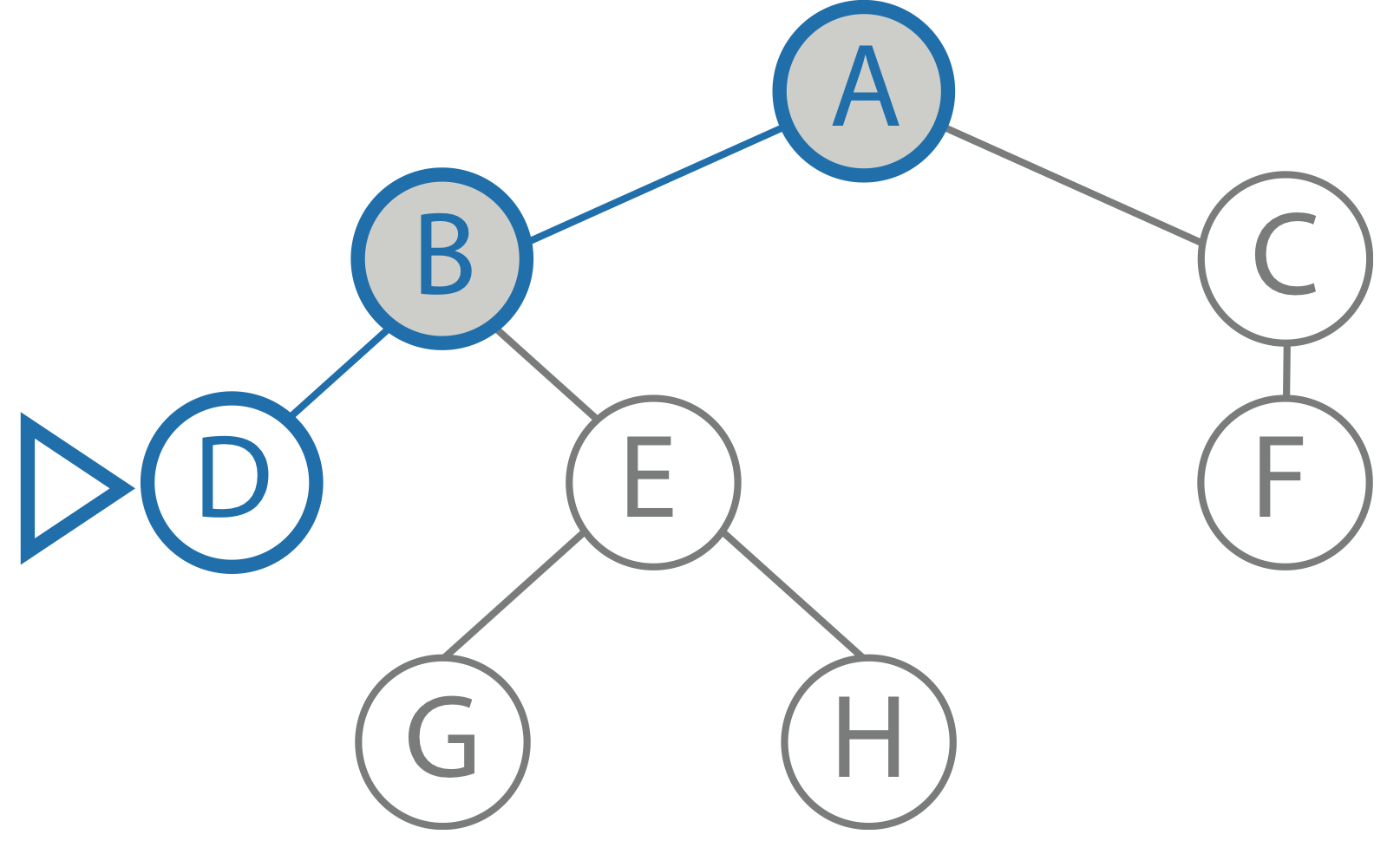 |
goal: F limit: 0 current path: A, B, D node: D child: - result: cutoff |
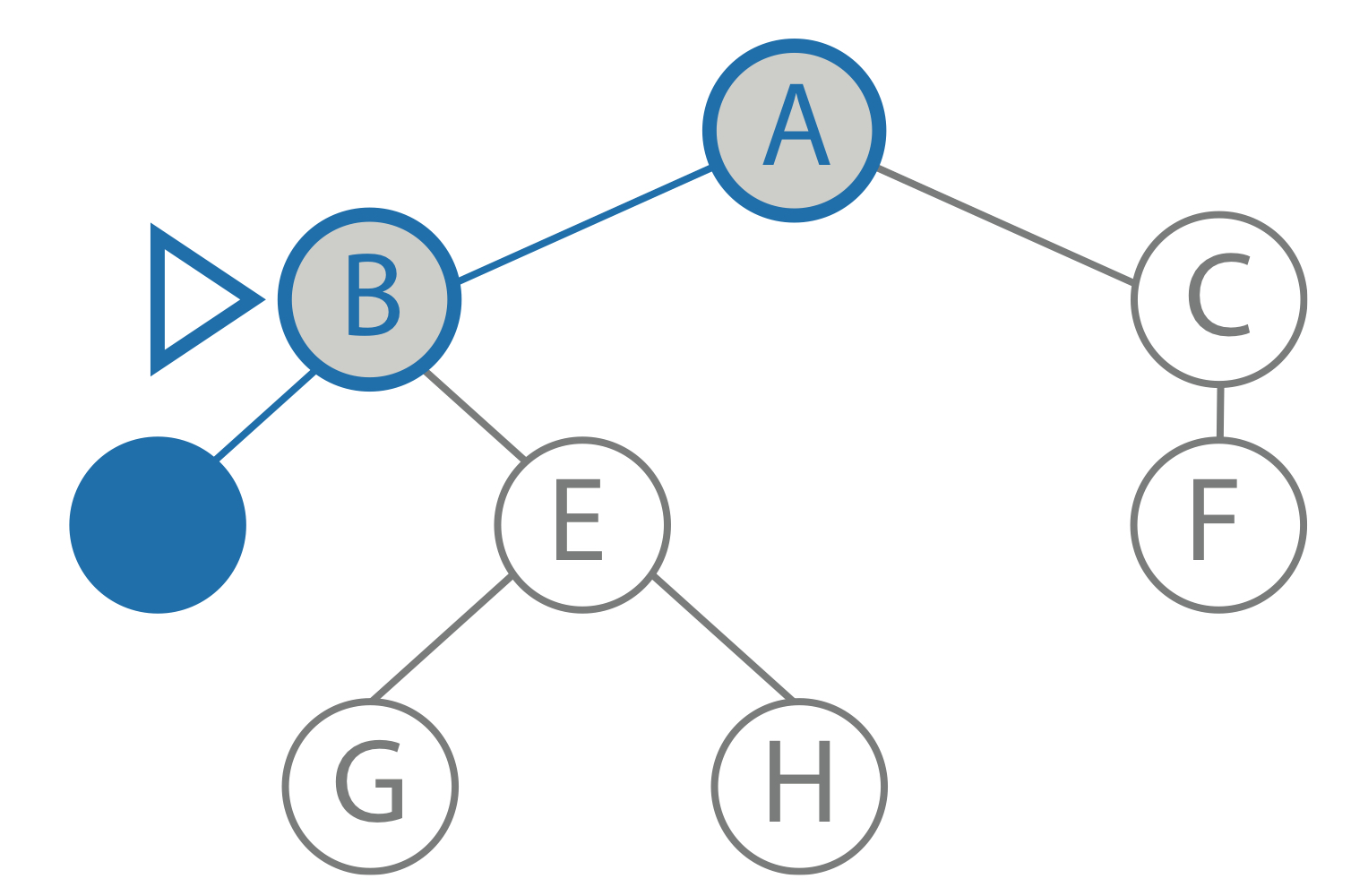 |
goal: F limit: 1 current path: A, B node: B child: D result: cutoff |
 |
goal: F limit: 1 current path: A, B node: B child: E result: to be computed |
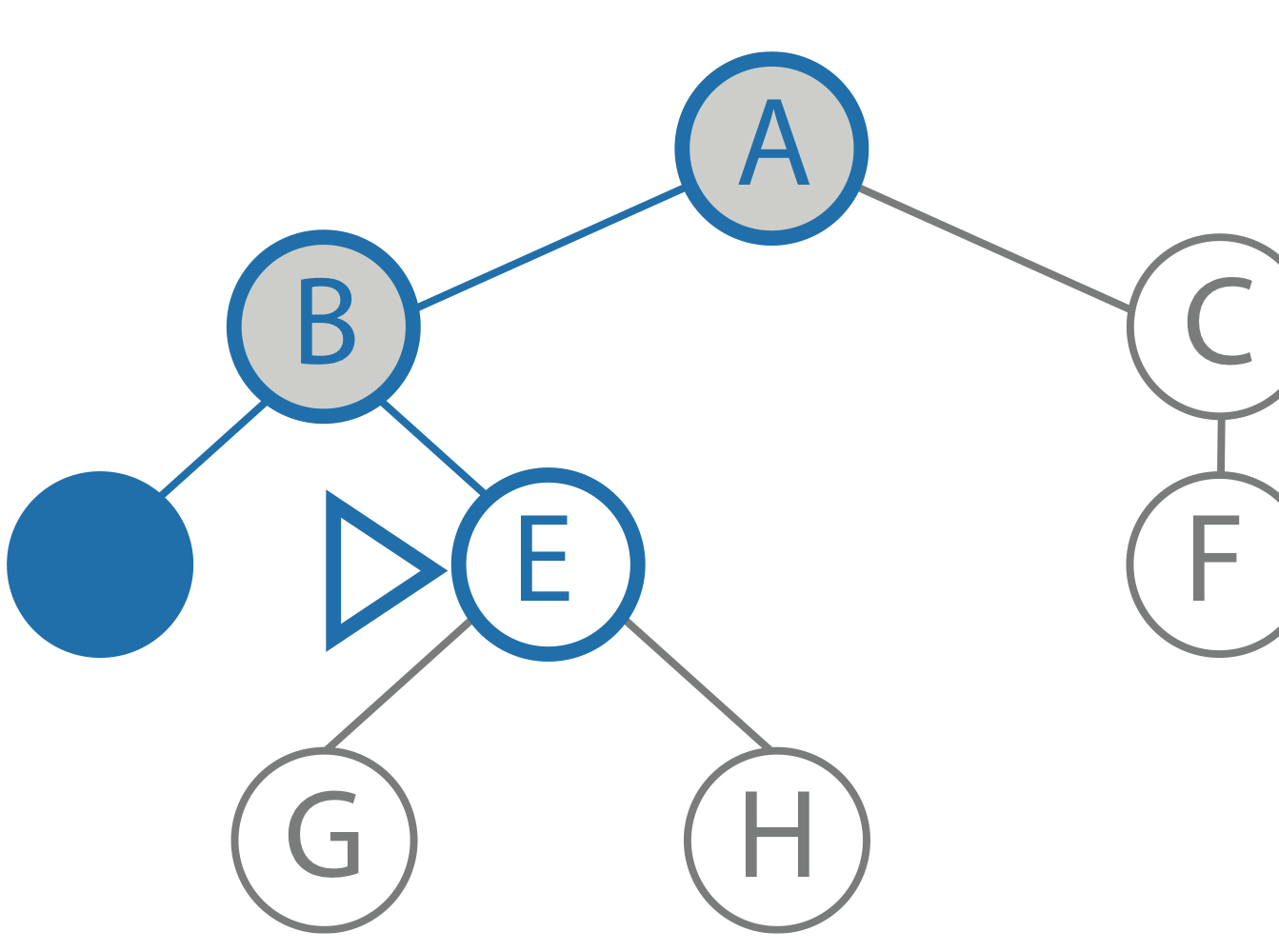 |
goal: F limit: 0 current path: A, B, E node: E child: - result: cutoff |
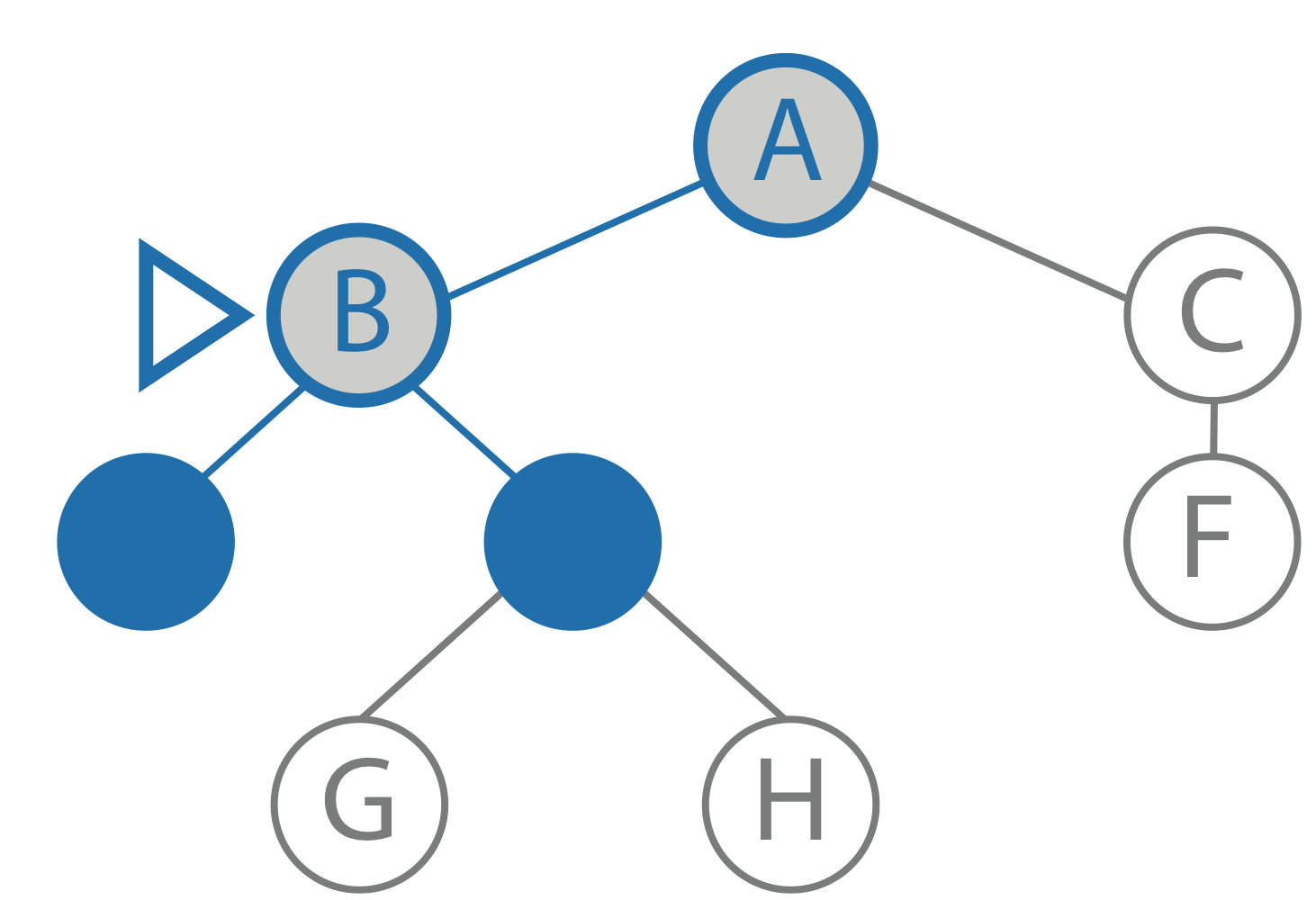 |
goal: F limit: 1 current path: A, B node: B child: E result: cutoff |
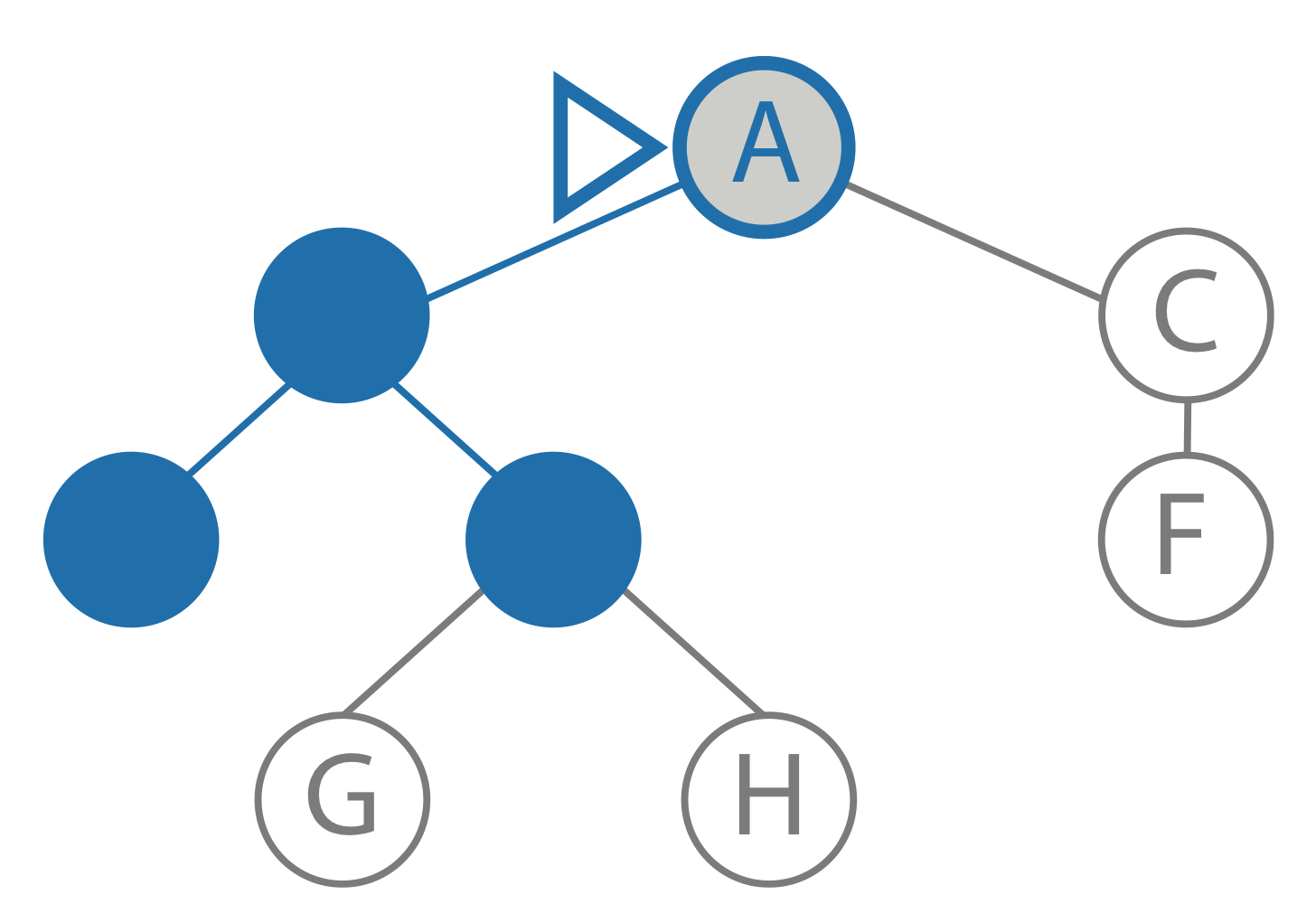 |
goal: F limit: 2 current path: A node: A child: C result: to be computed |
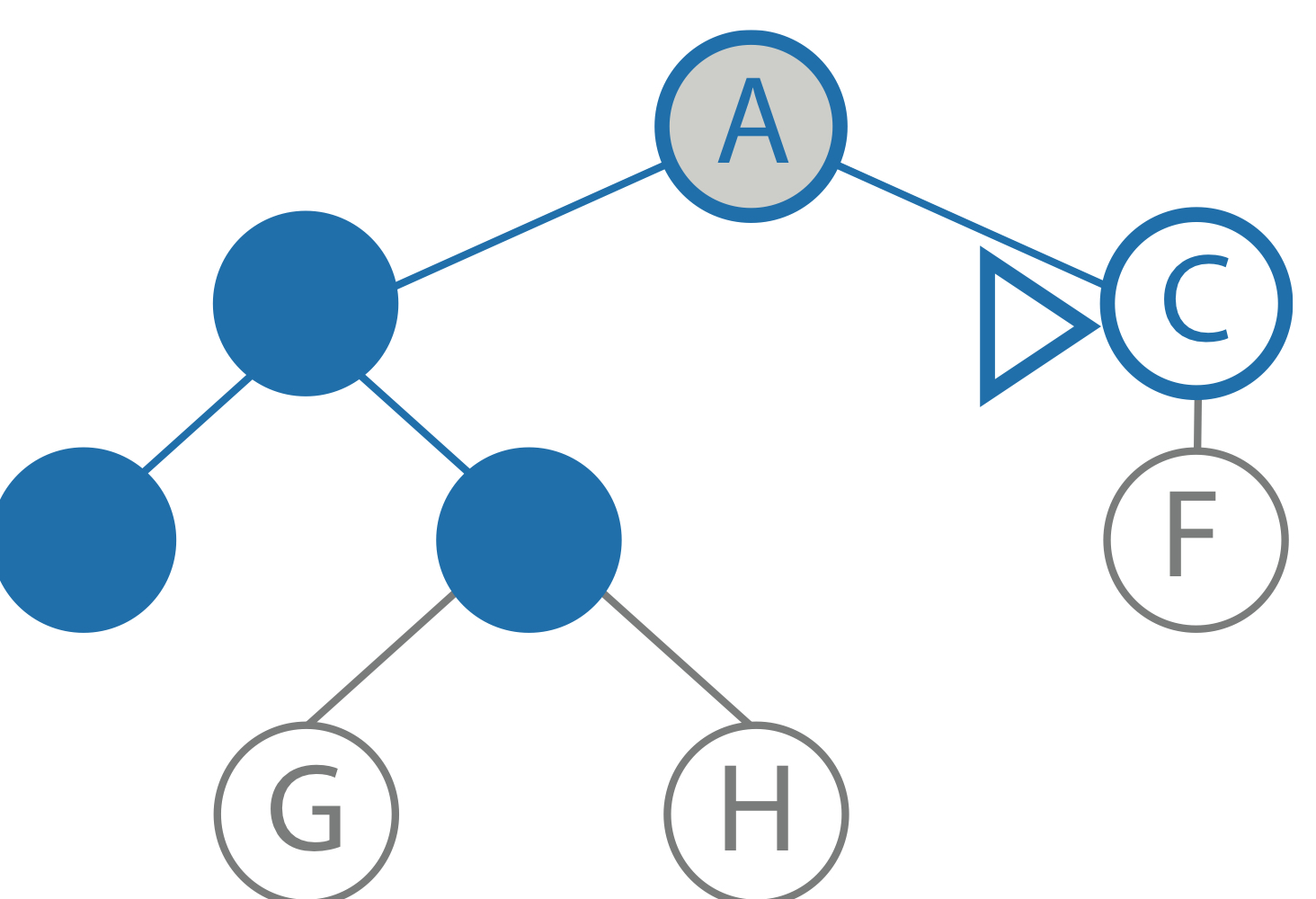 |
goal: F limit: 1 current path: A, C node: C child: F result: to be computed |
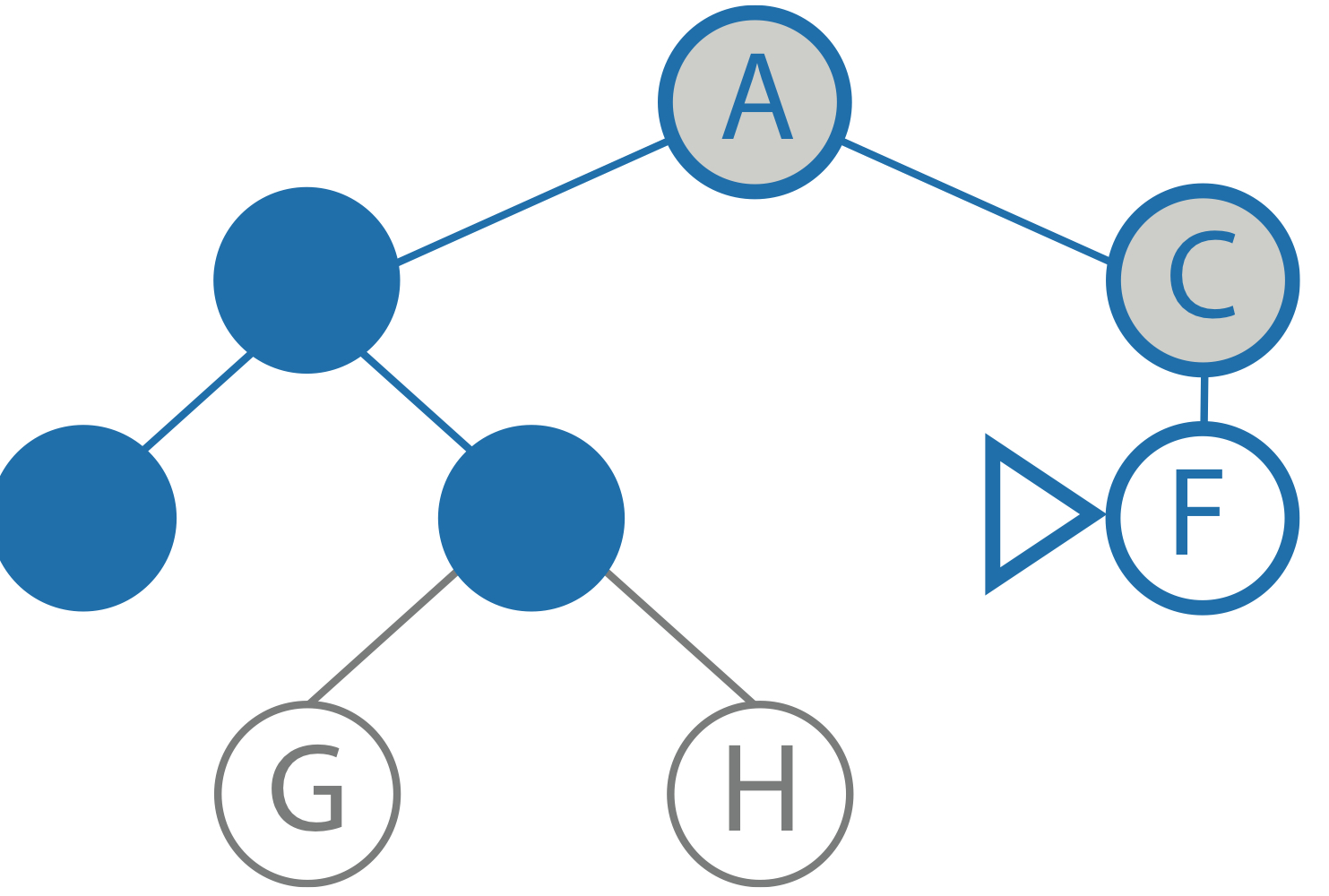 |
goal: F limit: 0 current path: A, C, F node: F child: - result: F |
 |
goal: F limit: 1 current path: A, C, F node: C child: F result: F |
 |
goal: F limit: 2 current path: A, C, F node: A child: C result: F |
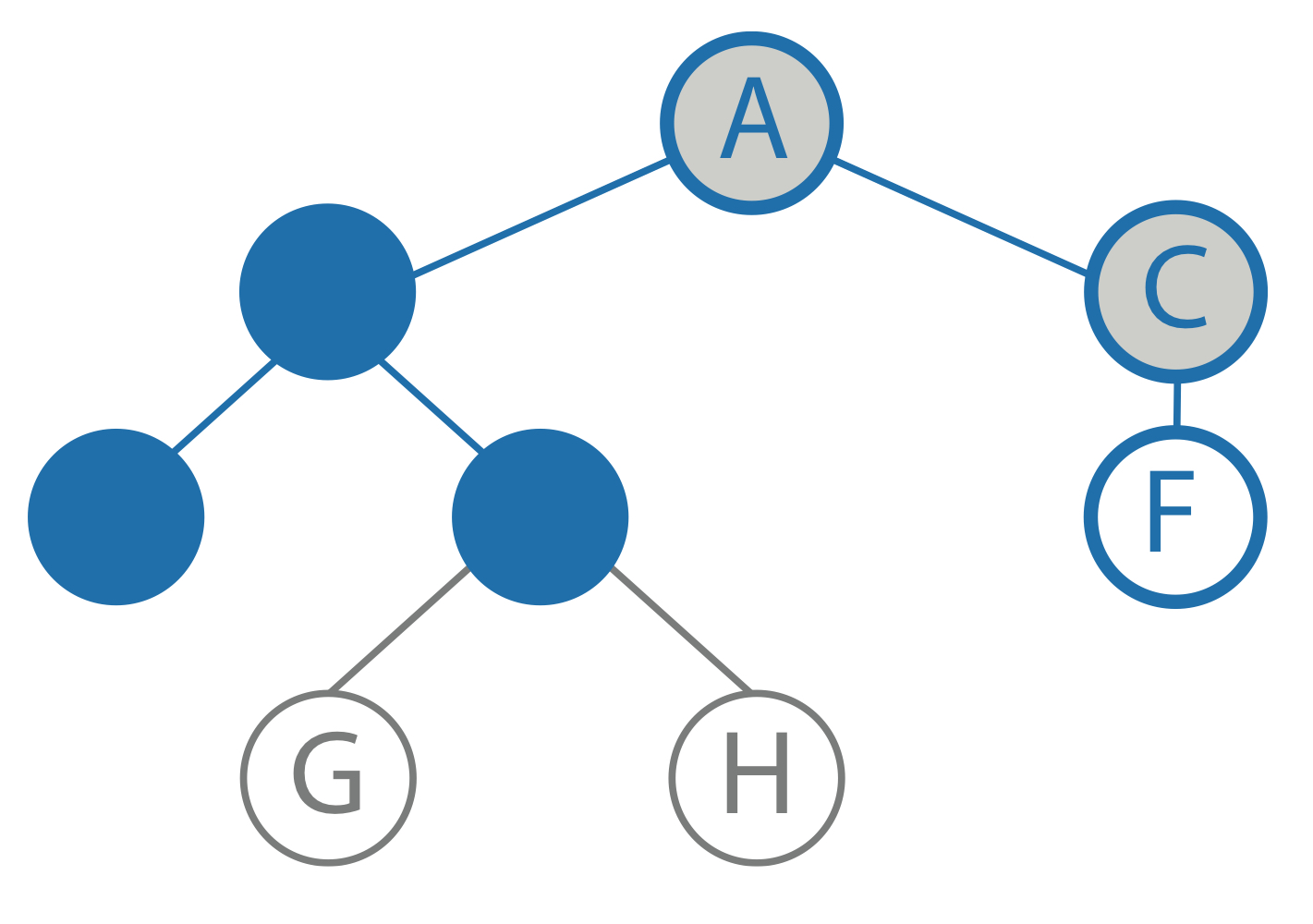 |
goal: F limit: 2 |
Depth-Limited Search Performance
Reminder: Branching factor \( b \), depth \( d \), maximum length \( m \) of any path, and dept limit \( I \).
- Complteteness: No, if \( I < d \) / 리밋이 깊이보다 작을때는 리밋이하의 깊이는 무시한다. 그러므로 답을 보장할 수 없다.
- Optimality: No, if \( I > d \) /만약 리밋이 깊이보다 크면 모든 노드와 + \({\alpha}\) 를 모두 고려해야 하므로 최적화는 아니다.
- Time complexity: Same as for DFS, but with \( I \) instead of \( m : O(b^I)\)
- Space complexity: Same as for DFS, but with \( I \) instead of \( m : O(bI)\)
결국 DLS에서는 리밋값을 어떻게 정하는가가 매우 중요해진다.
리밋값 \( I \)가 너무 작으면 답을 찾지 못하고 너무 크면 시간이 오래걸린다. Search의 Space 의 지름을 알고 있으면 리밋값을 설정하기 좋다. (\( {\approx} \) informaed search)
Iterative Deepening Search
Idea & Algorithm:
Shortcoming in DLS: One typically does not know the depth \( d \) of the goal state. /일반적으로 goal의 깊이를 알 수 없다.
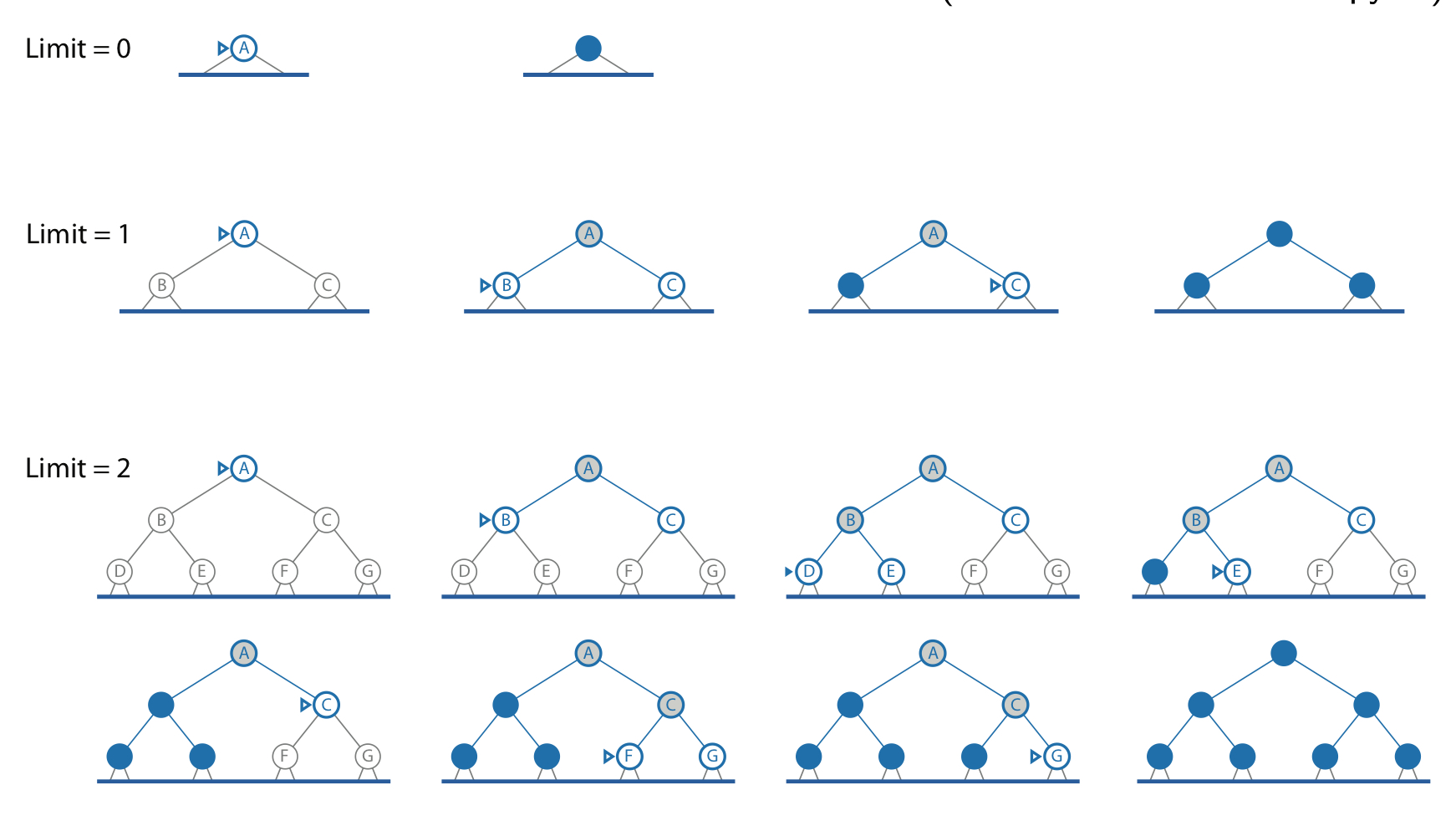
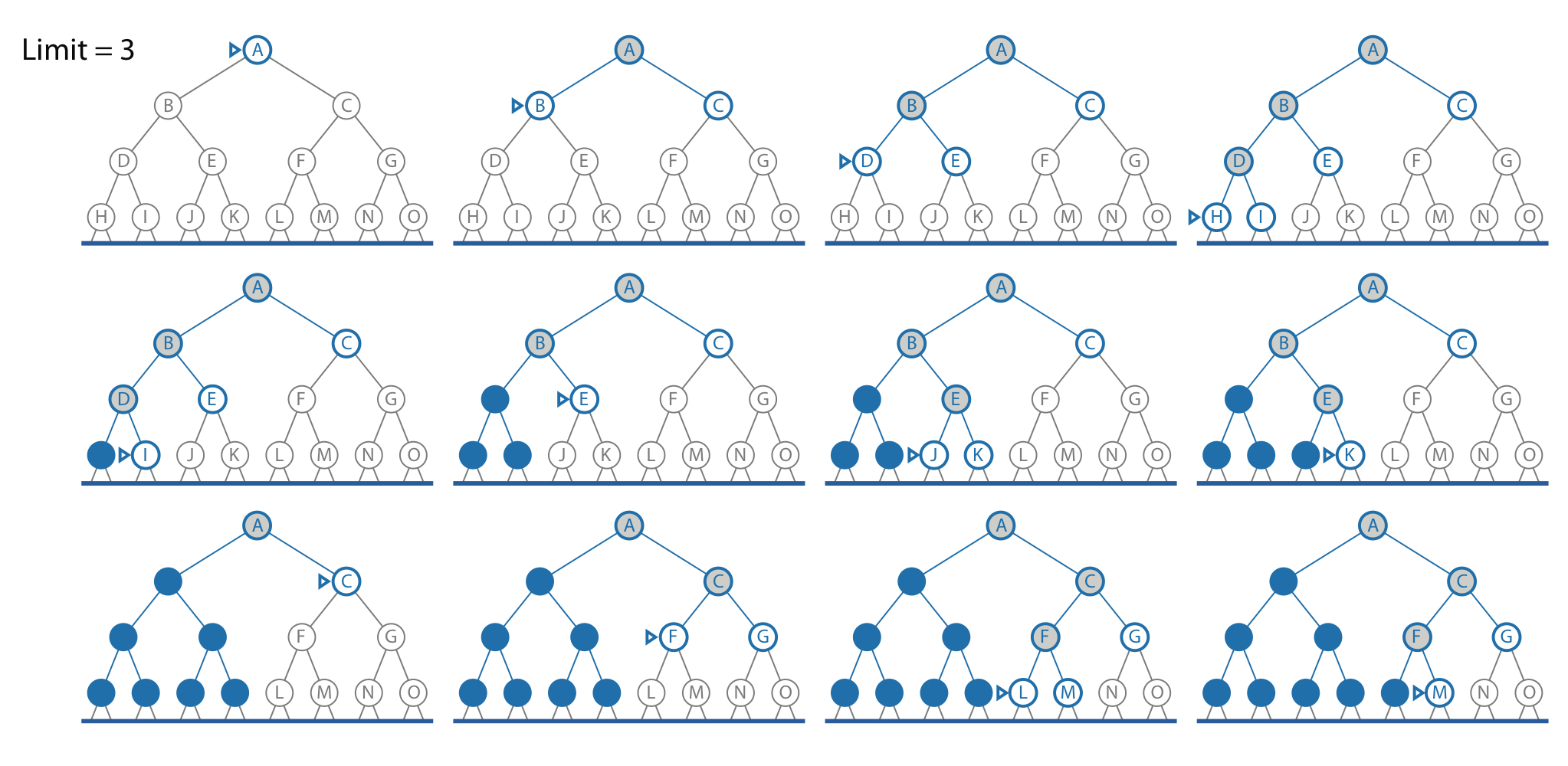
Solution: Use DLS and iteratively increase the depth limit \( I \).
/ 결국 IDS는 depth limit을 0, 1, 2, ...로 하나씩 증가시키면서 DFS를 여러번 실행하는 방법이다.
function Iterative-Deepening-Search returns a solution or failure
for depth = 0 to \( {\infty} \) do
result \( {\leftarrow} \) Depth-Limited-Search(promblem, depth)
if result \( {\neq} \) cutoff then return result
Iterative Deepening Search Performance
Reminder: Branching factor \( b \), depth \( d \), maximum length \( m \) of any path, and dept limit \( I \).
- Complteteness: Yes, if depth \( d \) of the goal state is finite / 깊이가 유한할때는 답을 보장 할 수 있다.
- Optimality: No in gerneral, Yes, if cost= 1 per step /iterative반복 하면서 탐색을 하기 때문에 일반적으로 옵티말하지는 않다. 그러나 각각의 줄기 비용이 1일 경우는 옵티멀.
- Time complexity: 가장 깊은 노드는 1번,그 다음 수준의 노드는 2번 생성되며.... 총 \( d \) 번 생성된다. / BFS와 같다.
$$ (d)b + (d - 1)b^2 + (d - 2)b^3 + ... + (1)b^d = O(b^d) $$
- Space complexity: Same as for DFS, but with \( d \) instead of \( m : O(bd)\)
Comparison of Computational Effort
The intuition that the iterative deepening search requires a lot of time is wrong. The search whthin the lighest level is dominating.
/ IDS의 시간이 오래 걸릴것이라는 직감이 있는데, 편견에 불과하다. 실제로는 가장 라이트한 수준에서 검색이 지배적이다.
Example:
\( b= 10, d= 5\), solution at far right leaf:
Breadth-First Search
$$ b + b^2 + b^3 + ... + b^d $$
$$ =10 + 100 + 1000 + 10000 + 10000 = 111110 $$
Iterative Deepening Search
$$ (d)b + (d - 1)b^2 + ... + (1)b^d $$
$$ 5x10 + 4x100 + 3x1000 + 2x10000 + 1x100000 = 123450 $$
The difference is almost negligible and becomdes relatively smaller, the larger the problem is. /예시를 보면 차이가 그렇게 크지는 않다. 그러나 수가 커질수록 차이도 커질 수 있다.
Bidirectional Search
- Idea: main idea is to run two searches. One freom the initail state andone backwared freom the goal, hoping that both searches meet in the middle.
- Motivation: This is also visualized in the figure, where the area from boteh search trees together is smaller than freom one treereaching the goal:
$$ b^{\frac{d}{2}} +b^{\frac{d}{2}} < b^d $$

it requires one to "search backwards"
- Easy: When all actions are reversible and there is only one goal, (ex. 8-puzzle, Holiday in Romania) it is easy to find the answer.
- Difficult: When the goal is an abstract description and thereiexist many goal states. (ex. 8-Queens)
Comparing Uninformed Search Strategies
| BFS | UCS | DFS | DLS | IDS | |
| Compelete | \( Yes^a \) | \( Yes^{a,b} \) | No | Yes, if \(I {\geq} d\) | \( Yes^a \) |
| Optimal | \( Yes^c \) | \( Yes \) | No | No | \( Yes^c \) |
| Time | \( O(b^d)\) | \( O( b ^ {1 + \frac{a}{{\epsilon}} } ) \) | \( O(b^m)\) | \( O(b^I)\) | \( O(b^d)\) |
| Space | \( O(b^d)\) | \( O( b ^ {1 + \frac{a}{{\epsilon}} } ) \) | \( O(bm)\) | \( O(bI)\) | \( O(bd)\) |
\( a \) : compete if \( b \) is finite
\( b \) : compete if step costs \( {\geq} {\epsilon} \) for positive \({\epsilon} \)
\( c \) : optimal if all step costs are identical
Summary Keywords
- the initial state, actions, transition model, a goal test function, a path cost funtion
- completeness, optimality , time complexity, space complexity
- Breath-First search
- Uniform-Cost serach
- Depth-First search
- Iterative deepening search
- Bidirectional search
'All About ECE > Artificial Intelligence' 카테고리의 다른 글
| [AI/인공지능] Informed Search (0) | 2022.12.16 |
|---|---|
| [AI/인공지능] Breadth-First Search, Uniform-Cost Search, Depth-First Sesarch (0) | 2022.12.16 |
| [AI/인공지능] How to formulate Problems, Example, Searching for Solution, Do the right Thing (0) | 2022.12.16 |
| [AI/인공지능] Intelligent Agents (0) | 2022.12.14 |
| [AI/인공지능] Introduction to AI (0) | 2022.12.14 |




댓글