Organization
1. Informed Saerch Strategies
1) Greedy Best-First Search
2) A* Search
2. Heuristic Functions
1) Relaxed Problems
2) Pattern Databases
3) Reachablity Analysis
Informed Search
- uninformed search와 비교시, informed seach uses indictaions how promising a state is to reach a goal
- Can find solutions more efficiently than uninformed search
- The choice of the next node is based on an evaluation function \(f(n) \), which itself is often based on a heuristic function \( h(n) \)
- \( h(n) \) is problem specific with the only constraints that it is nonnegative and \( h({\hat{n}}) = 0 \). where \( {\hat{n}} \) is a goal node.
Heuristics refers to the art of achieving good solutions with limited knowledge and time based on experience.
/경험을 바탕으로 최적화 된 솔루션을 얻는 방식.
Greedy Best-First Search
한국어로 하면 설마 리얼 욕심쟁이 최상 우선 선택 탐색...?????(당황스럽다)
Idea: using the heuristic function such that \( f(n) = h(n) \)
Think about Holiday-in-Romania Example agein.
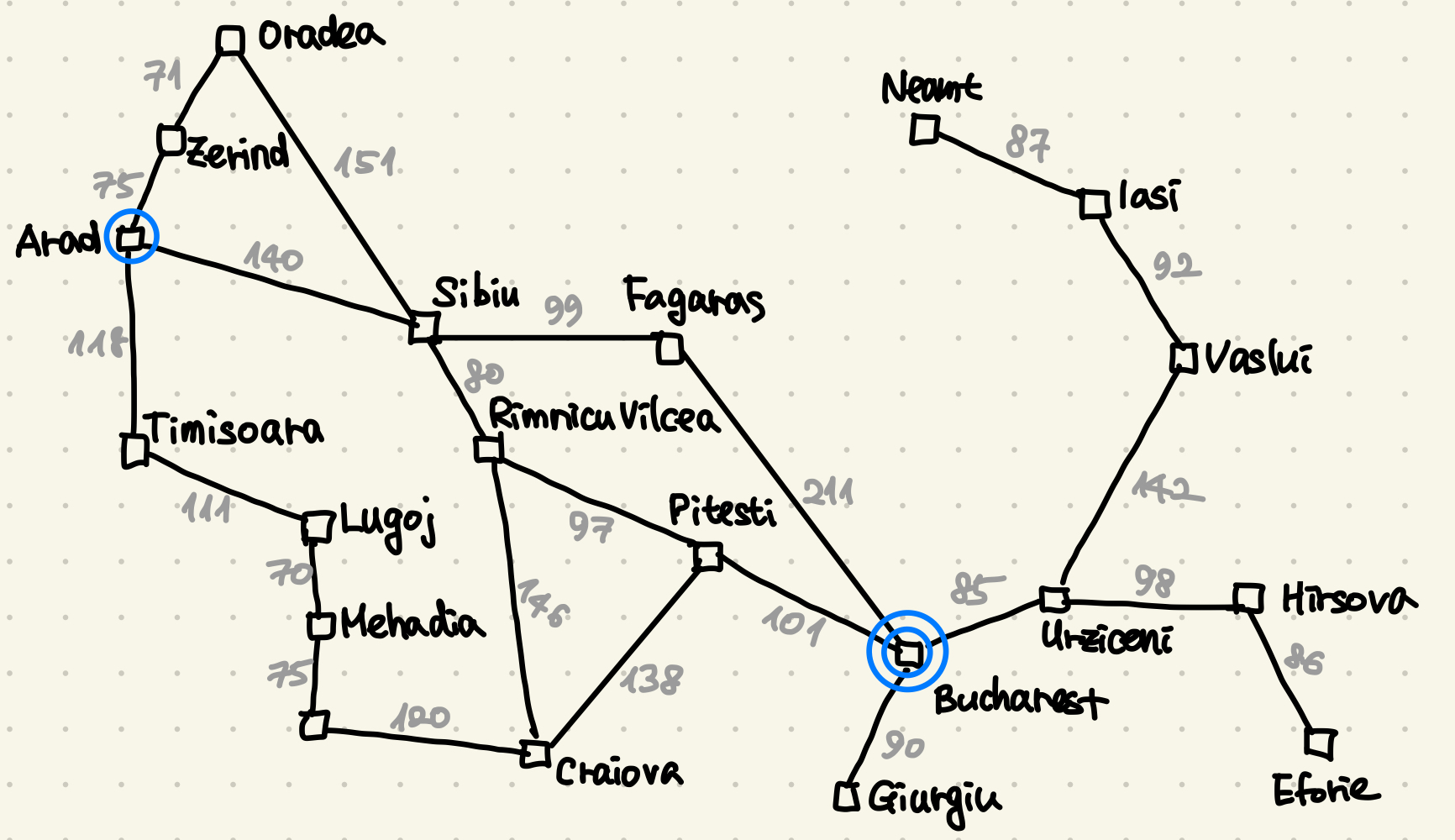
We use the stragiht line distance to the goal as \( h(n) \)




항상 옵티멀한 탐색은 아니다. 32km longer than througth Rimnicu Vilcea ans Pitesti.
Greedy Best-First Search는 항상 답을 찾을수 있는것은 아닌데, explored set을 쓰는경우이다. 이 경우에는 유한한 state여도 답을 보장받지 못한다.
예를들어 From lasi to Faragas. Neamt is first expanded due to closer straight line distance and then constantly moves between lasi and Neamt.
Greedy Best-First Search Performance
Reminder: Branching factor \( b \), depth \( d \), maximum length \( m \) of any path.
- Completeness: Yes, if graph search is used
- Optimality: No
- Time complexity: 가장 마지막에 답을 찾도록 유도 되었을때가 worst-case이다. \( O(b^m) \) 그러나 보통은 매우 드라마틱한 양상을 보여준다.
- Space complexity: same as time complexity \( O(b^m) \)
A* Search (A-star search)
Idea: 함수를 다음과 같이 정의한다. 지금까지 온 길 \( g(n) \) 과 앞으로 가야할 길 \(h(n) \)의 합으로 정한다.
\( f(n) = g(n) + h(n) \)
the best way = the way so far + the way to the goal
그리고 \( h(n) \)에 조건이 하나 붙는데, 예상하는 값이 실제 값보다 작아야한다.
\( {\rightarrow} f(n) \) never overestimates the cost to the goal and thus the algorithm keeps searching for paths with a lower cost to the goal.
Consistent Heuristics
A slightly stronger condition called consistency is required when applying A* to graph search. / 이 휴리스틱에 컨시스트라는 조건을 붙여본다. 즉,
$$ h(n) {\neq} c(n, a, n{\prime}) + h(n{\prime}) $$
It is fairly easy to show that every consistent heuristic is also admissible.
 |
 |
 |
 |
 |
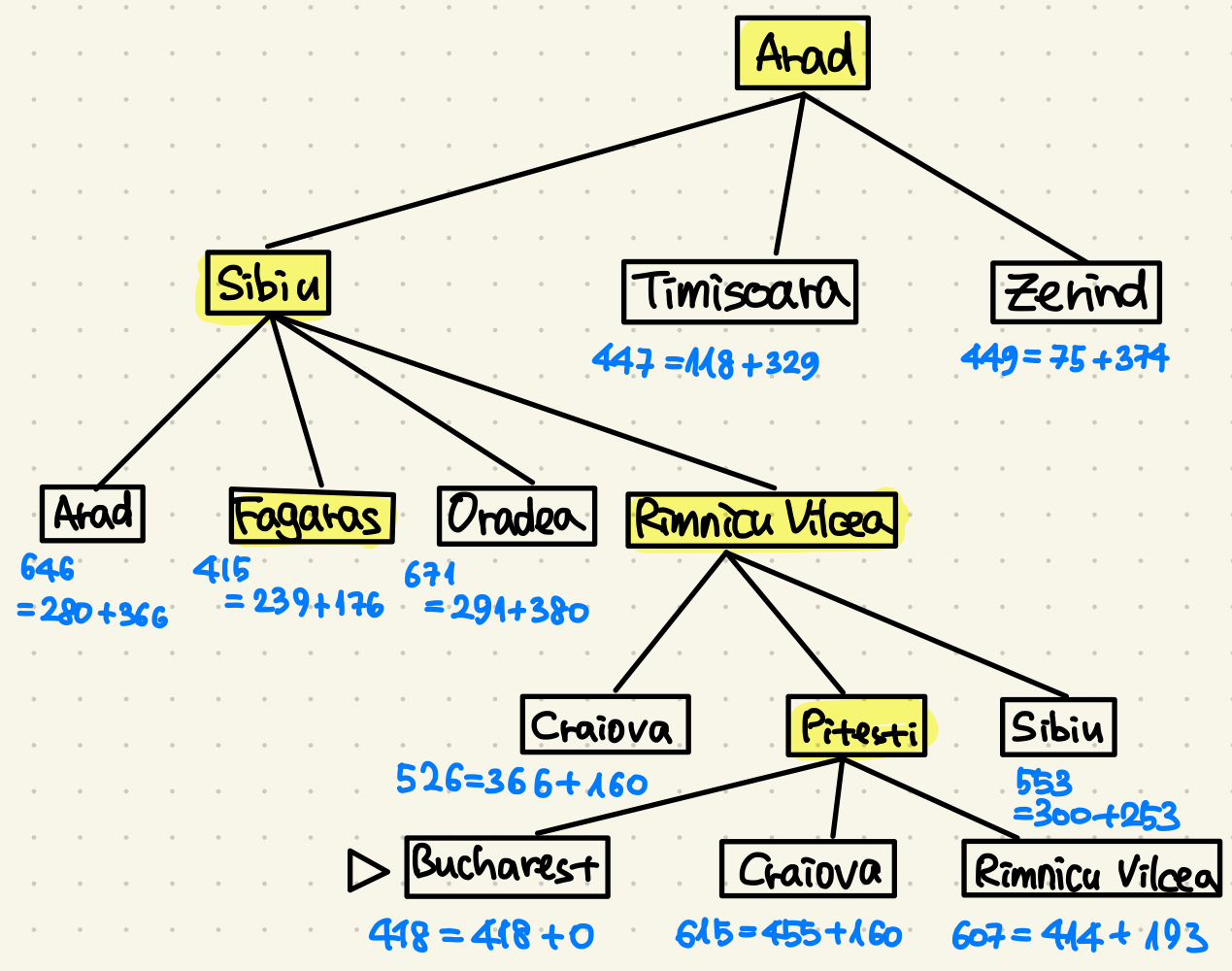 |
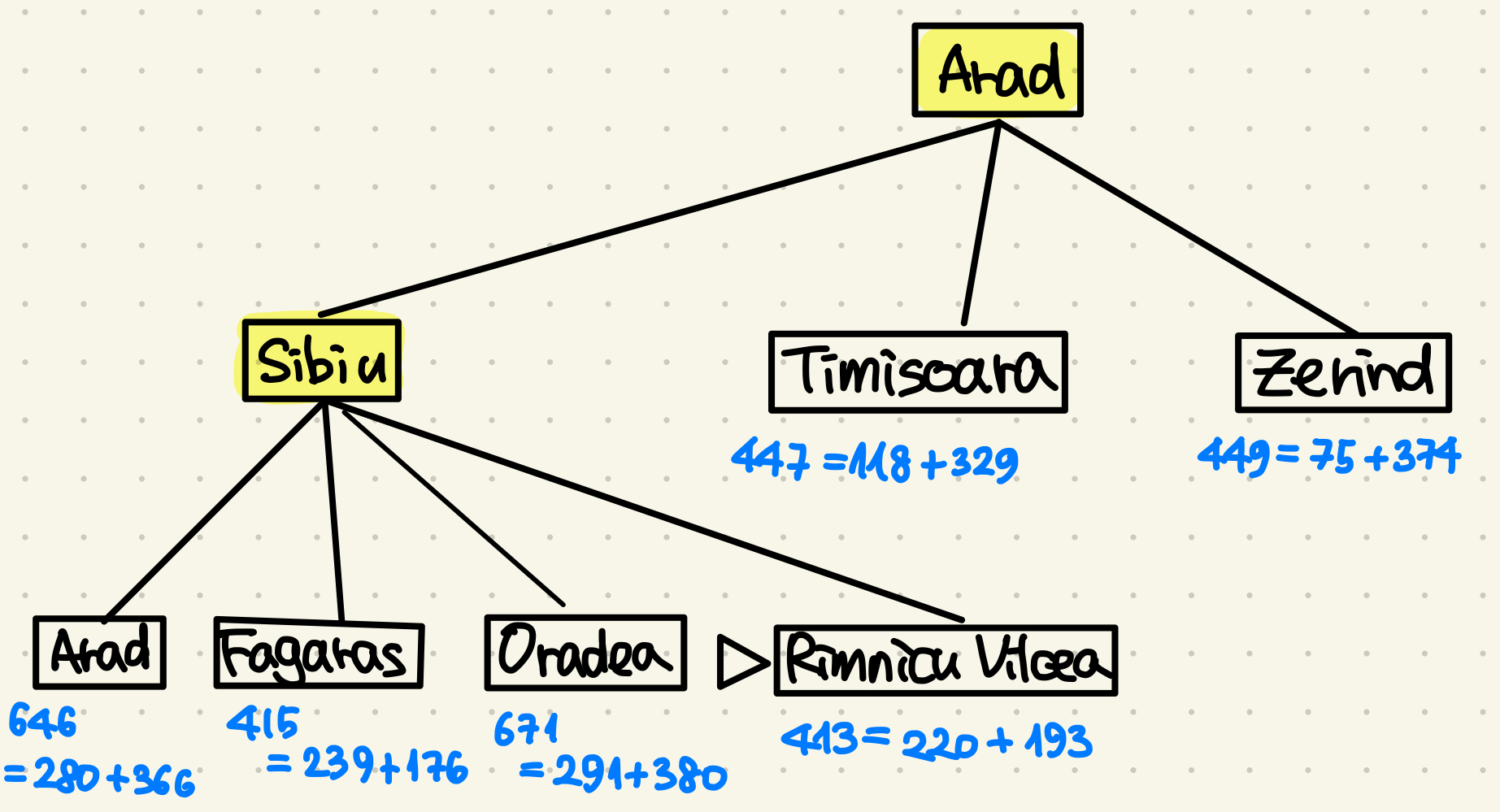
Nodes are labeled with \( f = g + h \)
A* Search : Effects of the Heuristic A*
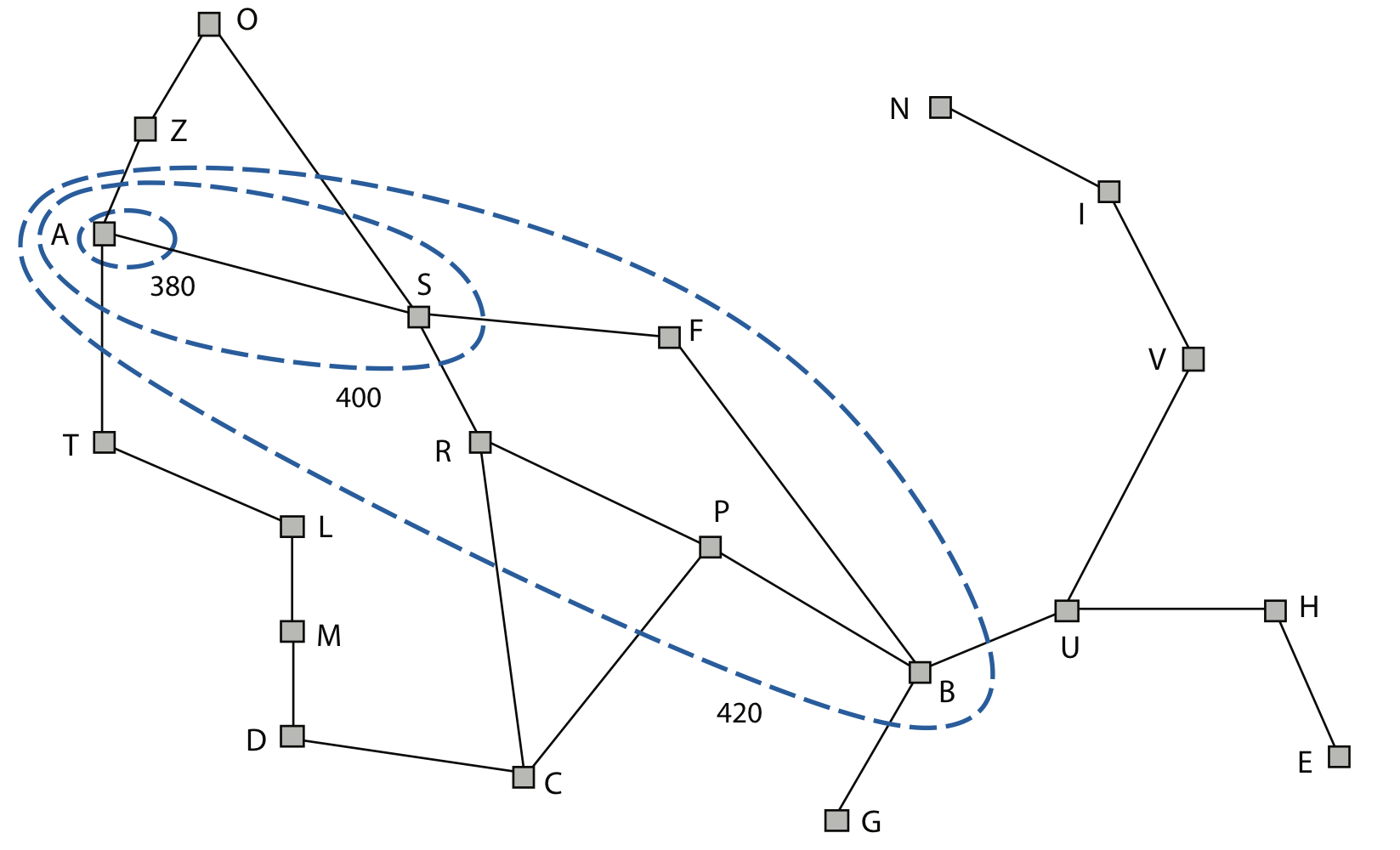
- The heuristic "steers" the search towards the goal.
- A* expands nodes in order of increasing \( f\) value, so that "\(f\) -contours" of nodes are gradually added.
- Each contour \( i \) includes all nodes with \( f {\leq} f_i \) , where \( f_i < f_{i+1} \)
A* Search: Pruning
1) Given the cost C* of the optimal path, only path with \( f(n) {/leg} C* \) are expanded.
\( {\rightarrow} \) A* never expands nodes, where \( f(n) < C* \)
2 ) The concept of pruning - elimination possibilites from consideration without having to examine them - brings enormous time saving and is similary done in other areas of AI
A* Search Performance
Reminder: Branching factor \( b \), depth \( d \), maximum length \( m \) of any path.
Time complexity와 Space complexity는 relative error를 통해 표기한다.
relative error \( {\epsilon} = \frac{h* - h}{h*} \)
- Completeness: Yes, 비용이 0 보다 클 경우 답을 보장받는다
- Optimality: Yes 휴리스틱은 써치트리의 옵티멀을 위해 만들어짐.
- Time complexity: \( O(b^{{\epsilon}d}) \)
- Space complexity:
이 외에 추가로 에이써치의 베리에이션도 있다.
Alternatives of A* Search
Iterative-deepening A*
Recursive best-first search
Memory-bounded A*
Heuristic Functions for the 8-Puzzle

Two commonly used candidates that underestimate the costs to the goal:
- \( h_1 \) : the number of misplaced tiles - e.g. in the figure \( h_1 \) = 8 / goal state와 다르게 놓인 state들의 타일 갯수
- \( h_2 \) : the sum of the horizontal and vertical distances to the goal: / goal state까지의 step의 합
| tile | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | sum |
| steps | 3 | 1 | 2 | 2 | 2 | 3 | 3 | 2 | 18 |
Domination of a Heuristic
여기서 하나의 의문점이 생기는데, 그렇다면 항상 \( h_2\)가 \( h_1 \)보다 낫거나 혹은 비슷하게 좋은가? 라는 점이다.
For every node, we have \( h_2(n) {\geq} h_1 \). So we say that \( h_2\) dominates \( h_1 \) .
A* using \( h_2 \) will never expand more nodes than with \( h_1 \) - except possibly for some nodes with \( f(n) = C* \) .
\( {\rightarrow} \) 항상 \( h_2\)가 \( h_1 \)보다 낫거나 혹은 비슷하게 좋다. \( h_2\)는 \( h_1 \) 를 지배한다.
Heuristics from Relaxed Problems

Idea: The previous heuristics \( h_1\) and \( h_2\) are perfectly accurate for simplified versions of the 8-puzzle.
Method: Formalize a problm definition and remove restrictions.
Result:
- One obtains a relaxed problem, i.e. a problem with more freedom, whose state-space graph is a supergraph of the original one.
- The optimal solution in the original problem is automatically a solution in the relaxed problem, but the relaxed problm might have a better solution due to added edges.
- Hence, the cost of the optimal solution in the relaxed problem is underapproximative.
Example for 8-Puzzle
A tile can move from square A to B if \( {\Phi}_1 {\wedge} {\Phi}_2 \) , where
\( {\Phi}_1\): B is blank
\( {\Phi}_2\) : A is adjacent to B
We generate three relaxed problmes by removing one or two conditions:
- remove \( {\Phi}_1\) : A tile can move freom square A to B if A is adjacent to B
- remove \( {\Phi}_2\) : A tile can move freom square A to B if B is blank.
- remove all: A tile can move freom square A to B
- From the first relaxed problem, we can generate h2 and from the third relaxed problem, we can derive h1. /첫 번째에서 h2를 생성하고 세 번째에서 h1을 도출할 수 있다.
- If one is not sure which heuristic is better, one can apply in each step. /어떤 것이 더 나은지 확실하지 않은 경우엔 maximum으로 비교 후 사용한다.
$$ h(n) = max [h_1(n), h_2(n), ... , h_M(n) ] $$
Heuristics from Pattern Databases
Underapproximative heuristics can also be obtained freom subproblems.
Those solution cost are underapproximations and can be stored in a database.
The number of subproblmes has to be much less than the original problems to not exceed storage capacities.
Overview of Informed Search Methods

Summary
- Informed search methods require a heuristic function that estimates the cost \( h(n) \) from a node \( n\) to the goal:
1) Greedy best-first search expands nodes with minimal \( h(n) \) , which is not always optimal.
2) A* Search expands nodes with minimal \( f(n) = g(n) + h(n) \) . A* is complete and optimal for underapproximative \( h(n)\).
- The perfomance of informed search depends on the quality of the heuristic. Possibilites to obtain good heuristics are relaxed problems, pattern databases and reachability analysis.




댓글