4. Zufallsvariablen
4.1. Definition
gegeben: Wahrscheinlichkeitsraum \( ( \Omega, \mathbb{F}, \mathbf{P} ) \)
\(X : \Omega \mapsto {\Omega}' \) ist ZUfallsvariable, wenn für jedes Ereignis \( \mathbf{A'} \in \mathbb{F'} \) im Bildraum ein Ereignis \( \mathbf{A} \) im Urbildraum \( \mathbb{F}\) existiert, sodass \( \{ \omega \in \Omega | \mathbf{A'} \} \in \mathbb{F} \)

5. Wahrscheinlichkeitsverteilungen
5.0.1 Definition : Verteilung einer Zufallsvariable
$$ \mathbf{P}_X (A') = \mathbf{P}( \{ \omega \in \Omega | X(\omega) \in A' \} = \mathbf{P}( \{ X \in A' \} ) \forall A' \in \mathbb{F'} $$
5.0.2 Kumulative Verteilungsfunktion : Cumulative Distribution Fuction : KVF, CDF : 누적분포함수
$$ \mathbf{P}_X (A') = \mathbf{P}( \{ \mathbf{X} \leq x \}) $$
$$ \mathbf{P}(\{ \omega \in \Omega | X(\omega) \leq x \}) $$


Eigenschaften
- \( F_X (x) \) ist monoton wachsend
- \( F_X (x) \geq 0 \)
- \( F_X (x) \) ist rechtsseitig stetig:
$$ \forall h > 0 : \lim_{h \to 0}F_X (x + h) = F_X (x) : \forall x \in \mathbb{R} $$
- \( \lim_{x \to - \infty} F_X(x) = 0; \lim_{x \to \infty}F_X(x) = 1 \)
- \( \mathbf{P}(\{ a < X \leq b \}) = F_X(b) - F_X(a) \)
- \( \mathbf{P}( \{ X > c \}) = 1 - F_X(c) \)
5.0.3. Verteilung diskreter Zufallsvariablen
| Bezeichung | Abkürzung | Zusammenhang |
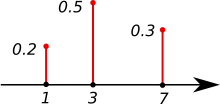
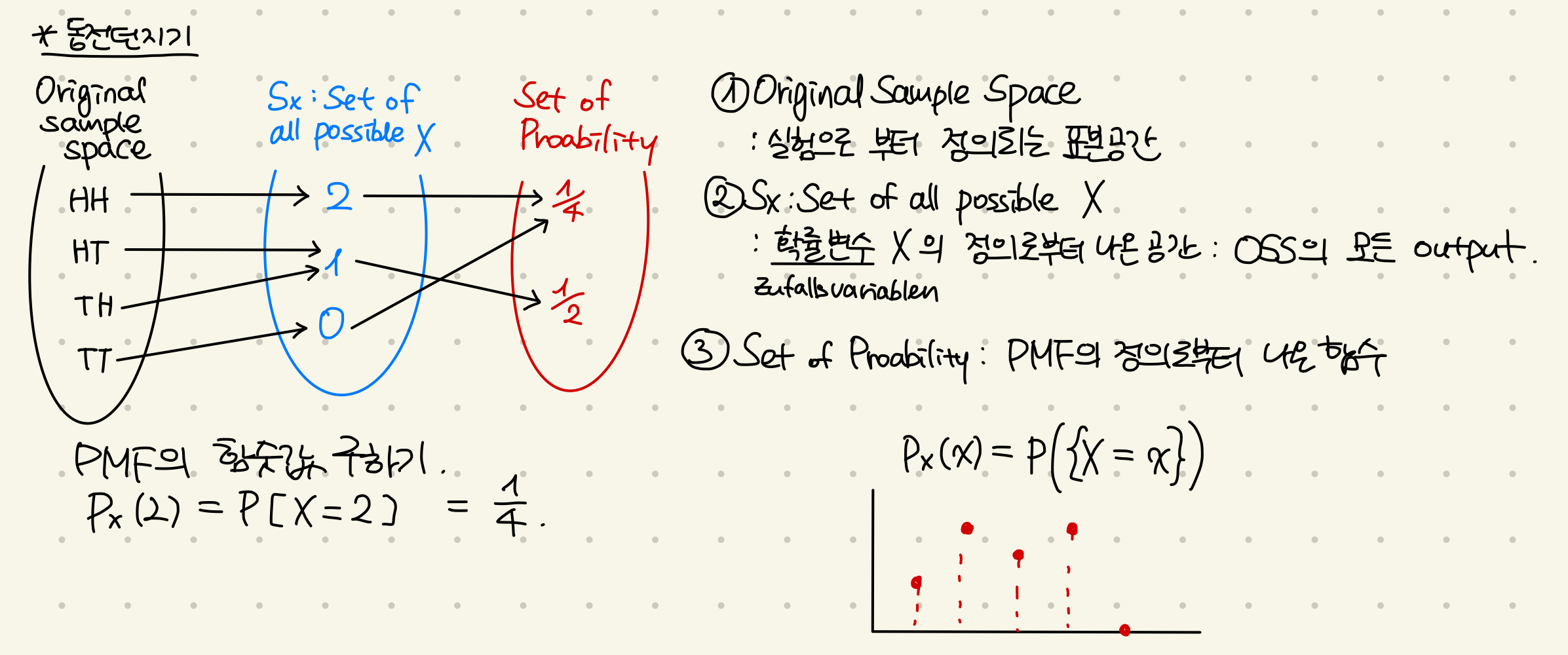
| Wahrscheinlichkeitsmassenfunktion | pmf | \( p_X(x) = \mathbf{P}(\{X = x\}) \) |
| Kumulative Verteilungsfunktion | cdf / kvf | \( F_X(x) = \sum_{\xi \in \Omega' : \xi \leq x }p_X(\xi) \) |
WMF / PMF : Probability Mass Fuction
5.0.4 Verteilung stetiger Zufallsvariablen
| Bezeichung | Abkürzung | Zusammenhang |
| Wahrscheinlichkeitsdichtefunktion | pdf / wdf | \( f_X(x) = \cfrac{d F_X(x)}{dx} \) |
| Kumulative Verteilungsfunktion | cdf / kvf | \( F_X(x) = \int_{-\infty}^x f_X(\xi) d\xi \) |
WMF / PDF : Probability Density Function
확률은 \( \mathbf{P}(\{ X \leq x\} )\)를 미분한 것이다
\( \cfrac{d}{dx} \mathbf{P}(\{ X \leq x \}) \)

dfdf

/




댓글